|
This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
|
=================================================================================
Phase identification is one of the most important applications of XRD technique. The typical procedure is:
i) Obtain an XRD pattern.
ii) Measure the d-spacings.
iii) Obtain the integrated intensities.
iv) Compare the obtained data with known standards, e.g. in the JCPDS (Joint Committee on Powder Diffraction Standards) file. Note that there are more than 50,000 JCPDS cards of inorganic materials.
The JCPDS committee was established to collect, edit, publish, and distribute primary references for X-ray powder diffraction analysis and identification of crystalline materials. This compilation has been commonly known as the Powder Diffraction FileTM (PDF).
The phase can be determined based on diffraction data such as XRD and electron diffraction patterns. For instance, if we know that a crystal has either BCC or FCC structure, the phase of the crystal can be determined by following steps:
i) Obtain the XRD peaks. The peaks are measured at 2θ angles of 40, 58, 73, 86.8, 100.4 and 114.7 °. The wavelength (λ) of X-ray used is 0.154 nm.
ii) As listed in page4825, the ratio of the first two sets of diffraction planes for FCC structures are {111) (A) and {200} (B), then we know,
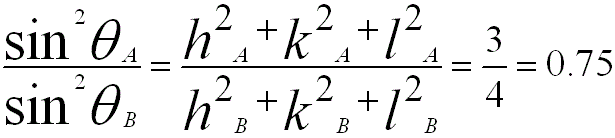 ----------------- [2497a] ----------------- [2497a]
Similarly, for BCC {110) (A) and {200} (B), we have,
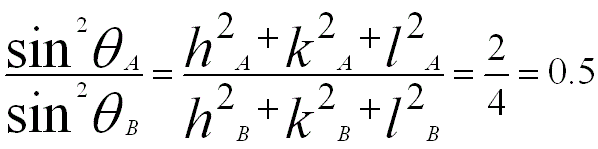 ----------------- [2497b] ----------------- [2497b]
iii) From the experimental data obtained in step i), we have,
| 2θ |
θ |
sinθ |
sin2θ |
| 40 |
20 |
0.3420 |
0.1170 |
| 58 |
29 |
0.4848 |
0.2350 |
| 73 |
36.5 |
0.5948 |
0.3538 |
| 86.8 |
43.4 |
0.6871 |
0.4721 |
| 100.4 |
50.2 |
0.7683 |
0.5903 |
iv) From the first and second angles in the table above, we can know that the ratio of the first two sets of diffraction planes for this crystal is 0.1170/0.3420 = 0.5.
v) Comparing with the calculation in step ii), we can know that the current crystal has BCC structure.
Note that, according to Bragg Condition, the lattice constant of BCC structure is given by,
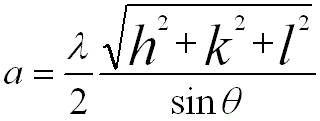 ----------------- [2497c] ----------------- [2497c]
|