|
This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
|
=================================================================================
It is necessary to eliminate all the second-order aberrations (highlighted in light orange in Table 3616) before correcting the third-order aberrations (highlighted in green in Table 3616), since the second-order aberrations are larger than the third-order aberrations caused by the rotationally symmetric fields.
Table 3616. Aberration Coefficient Nomenclature. The aberration coefficients have two
main types of notations, namely Krivanek notation, and Typke and Dierksen notation.
| Krivanek notation |
Typke and Dierksen notation |
Radial Order |
Azimuthal Symmetry |
Nomenclature |
| Ray |
Wave (k) |
| C0,1 |
A0 |
0 |
1 |
1 |
Image Shift |
| C1,2 |
A1 |
1 |
2 |
2 |
Two-fold axial astigmatism (or axial astigmatism of the 1st order) |
| C1,0 |
C1 |
1 |
2 |
0, ∞ |
Defocus (overfocus positive, or spherical aberration of the 1st order; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Δf) |
| C2,3 |
A2 |
2 |
3 |
3 |
Three-fold axial astigmatism (or axial astigmatism of the 2nd order)
|
| C2,1 |
B2 |
2 |
3 |
1 |
Axial coma |
| C3,4 |
A3 |
|
4 |
4 |
Four-fold axial astigmatism or axial astigmatism of the 3rd order Cs |
| C3,2 |
B3 |
|
4 |
2 |
Twofold astigmatism of Cs (or Third order twofold astigmatism, or Axial star aberration of the 3rd order) |
| C3,0 |
C3 |
|
4 |
0, ∞ |
Third-order spherical aberration (always positive for round lenses [3]; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Cs ) |
| C4,5 |
A4 |
|
5 |
5 |
Five-fold axial astigmatism or axial astigmatism of the 4th order |
| C4,1 |
B4 |
|
5 |
1 |
Fourth-order axial coma |
| C4,3 |
D4 |
4 |
5 |
3 |
Fourth order threefold astigmatism (or Three lobe aberration) |
| C5,6 |
A5 |
|
6 |
6 |
Six-fold axial astigmatism or sixfold axial astigmatism of the 5th order |
| C5,4 |
R5 |
5 |
6 |
4 |
Fourfold astigmatism of C5 (or Fifth order rosette aberration) |
| C5,2 |
S5 |
5 |
6 |
2 |
Twofold astigmatism of C5 (or Fifth-order axial star aberration) |
| C5,0 |
C5 |
|
6 |
0, ∞ |
Fifth-order spherical aberration |
| |
D5 |
|
|
|
Four lobe aberration of the 5th
order |
Sextupole elements can be conveniently used to produce three-fold symmetry of electromagnetic fields. The course of the deviation of the second order path along the optic axis depends on the arrangements and locations of both the round lenses and the sextupoles. These sextupole elements are normally employed in charged-particle optics to compensate for the primary second-order aberrations arising in the systems with a curved optical axis, such as spectrometers or imaging energy filters.
Sextupoles cannot be used to correct spherical aberrations if both the signs of the aberrations generated by sextupoles and round lenses are the same. Unfortunately, this is exactly the case if the second-order aberrations are eliminated. However, it is possible to reverse the sign of the spherical aberration by employing a round lens doublet. Figure 3616 shows the simplest system which can eliminate all second-order fundamental rays and thus all the second-order aberrations outside of the corrector. It consists of a round lens doublet and two identical sextupoles. The outer focal points of the corrector are the same as the nodal points N1 and N2 of the round lens doublet. The coils of the round lenses are connected oppositely in order to avoid an image rotation from the first sextupole, which is independent of the current strength. Therefore, the doublet images the front sextupole with magnification of −1 exactly onto the second sextupole centered about the nodal point N2 without introducing an off-axial third-order coma. This system can correct the third-order spherical aberrations of electron microscopes [1].
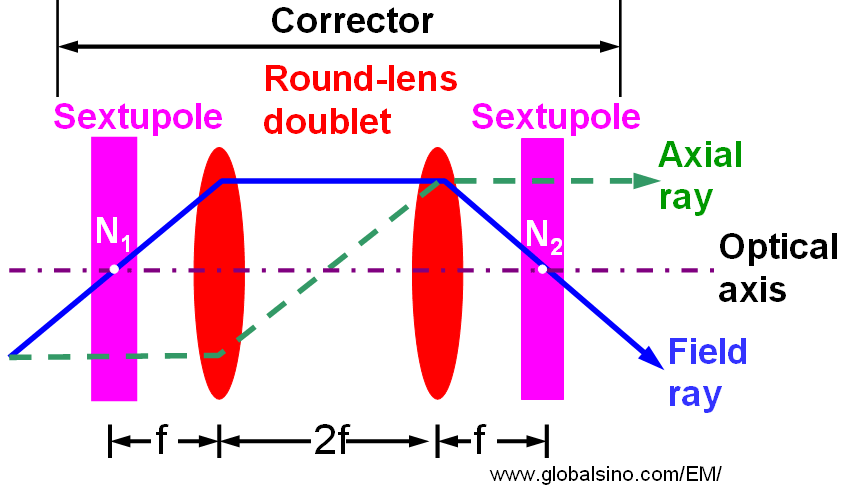
Figure 3616. Schematic illustration of a simplest spherical-aberration corrector. Adapted from [2].
[1] Born M. and Wolf E., 1975, Principles of Optics (Oxford:
Pergamon Press).
[2] Rose H. H., Optics of high-performance electron microscopes, Sci. Technol. Adv. Mater. 9 (2008) 014107.
[3] O. Scherzer, J. Appl. Phys. 20 (1949) 20.
|
