=================================================================================
A direct consequence of the decrease in beam energy, E0 is the correlated decrease in the penetration depth, R, of primary electrons (PE) interacting with the specimen. The basis of the combined directional elastic and inelastic scatterings along the direction of electron beam path can be described in simple analytical term proposed by Bethe equation in power law of the form[1],
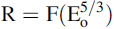 --------------------------[4795a] --------------------------[4795a]
The penetration of incident electrons is determined by the ‘electron stopping power’ of the specimen, which decreases with increasing atomic number (Z). Similar to Equation [4799a], the penetration depth of incident electrons can be given by Kanaya-Okayama Formula [2],
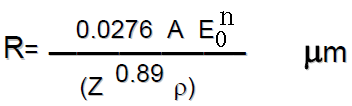 --------------------------[4795b] --------------------------[4795b]
R -- Depth Penetration
A -- Atomic Weight (g/mole)
n -- A constant
E0 -- Beam Energy (KV)
Z -- Atomic number
ρ -- Density (g/cm)2
n is often chosen to be ~1.35 when the primary beam energy E0 is < 5 keV, and be 1.67 when E0 > 5 keV. Figure 4795a shows log-log plot of the change of R as a function of the beam energy (E0) based on Equation 4795b. The difference of atomic densities between insulator and metals is a main factor inducing the difference of R. On the other hand, Figure 4795b shows the schematic of penetration depth and volume at different beam energies.
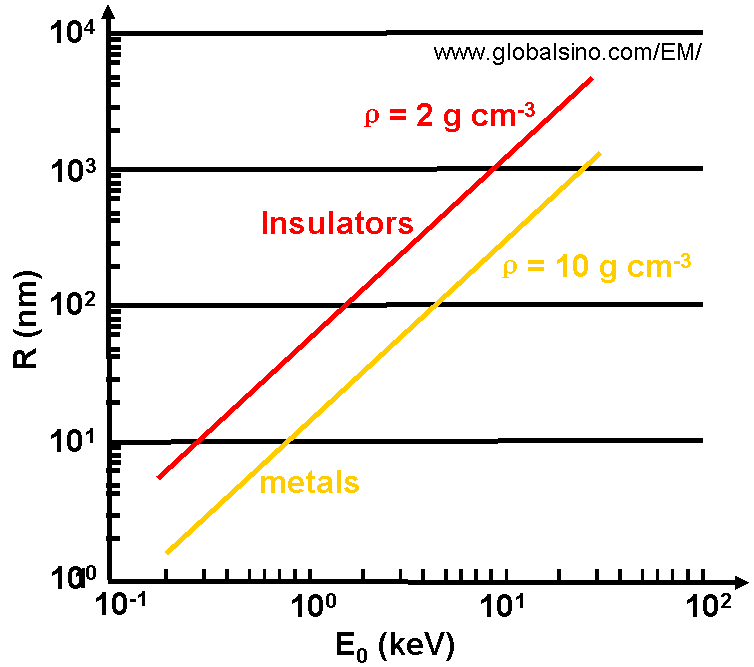
Figure 4795a. Log-log plot of the change of R as a function of the beam energy (E0)
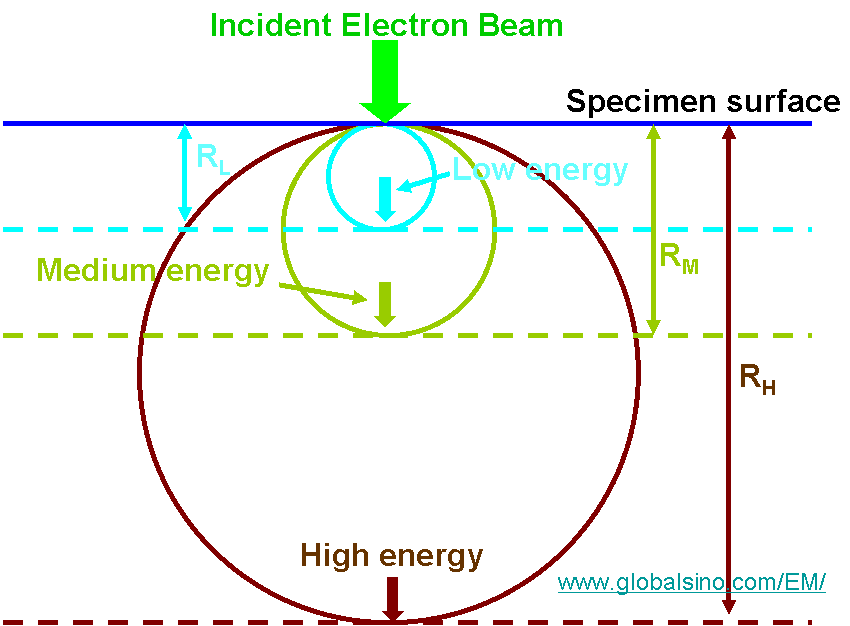
Figure 4795b. The schematic of penetration depth and volume at different beam energies.
Table 4795 gives some examples of penetration depths at some energy levels of incident beams in some elements. Furthermore, Figure 4795c shows the schematic of penetration depth and volume in comparison with escape depth.
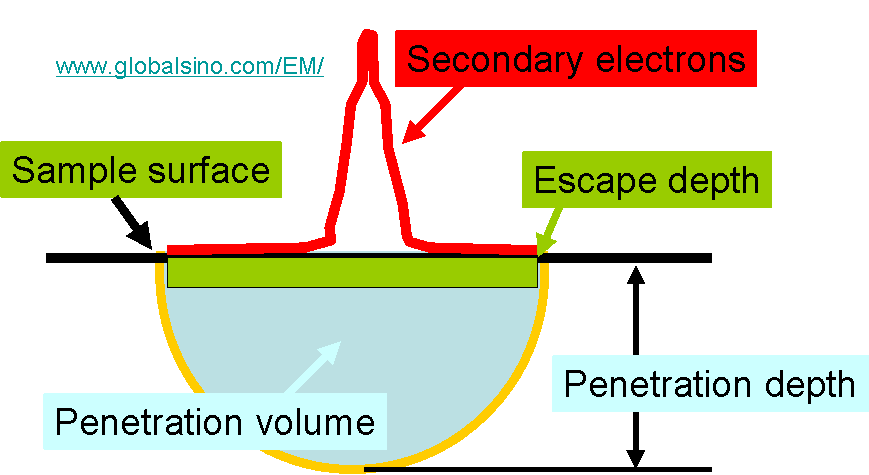
Figure 4795c. The schematic of penetration depth and volume in comparison with escape depth.
The high energy electrons, typically 100 – 300 keV, in a transmission electron microscope (TEM) can pass completely through a specimen at thicknesses below ~ 1μm. Because of the limit of specimen penetration, the effectively observable thickness increases ~3 to 10 times with voltage increase from 100 keV to 1 MeV in TEM.
Table 4795. Penetration depth of incident beams in EM. |
Beam energy |
0.5 keV |
1 keV |
2 keV |
5 keV |
10 keV |
15 keV |
30 keV |
| Angle |
0° |
0° |
|
0° |
0° |
0° |
0° |
| Polymer |
|
|
100 nm |
|
|
|
12 µm |
| 1 |
H |
|
|
|
|
|
|
|
| 2 |
He |
|
|
|
|
|
|
|
| 3 |
Li |
|
|
|
|
|
|
|
| 4 |
Be |
|
|
|
|
|
|
|
| 5 |
B |
|
|
|
|
|
|
|
| 6 |
C |
|
|
|
|
|
|
|
| 7 |
N |
|
|
|
|
|
|
|
| 8 |
O |
|
|
|
|
|
|
|
| 9 |
F |
|
|
|
|
|
|
|
| 10 |
Ne |
|
|
|
|
|
|
|
| 11 |
Na |
|
|
|
|
|
|
|
| 12 |
Mg |
|
|
|
|
|
|
|
| 13 |
Al |
|
|
|
400 nm |
|
2.4 µm |
|
| 14 |
Si |
|
|
|
|
|
|
|
| 15 |
P |
|
|
|
|
|
|
|
| 16 |
S |
|
|
|
|
|
|
|
| 17 |
Cl |
|
|
|
|
|
|
|
| 18 |
Ar |
|
|
|
|
|
|
|
| 19 |
K |
|
|
|
|
|
|
|
| 20 |
Ca |
|
|
|
|
|
|
|
| 21 |
Sc |
|
|
|
|
|
|
|
| 22 |
Ti |
|
|
|
|
|
|
|
| 23 |
V |
|
|
|
|
|
|
|
| 24 |
Cr |
|
|
|
|
|
|
|
| 25 |
Mn |
|
|
|
|
|
|
|
| 26 |
Fe |
35 Å |
10 nm |
25 nm |
160 nm |
|
990 nm |
1.8-3.1 µm |
| 27 |
Co |
|
|
|
|
|
|
|
| 28 |
Ni |
|
|
|
|
|
|
|
| 29 |
Cu |
|
|
|
150 nm |
|
900 nm |
|
| 30 |
Zn |
|
|
|
|
|
|
|
| 31 |
Ga |
|
|
|
|
|
|
|
| 32 |
Ge |
|
|
|
|
|
|
|
| 33 |
As |
|
|
|
|
|
|
|
| 34 |
Se |
|
|
|
|
|
|
|
| 35 |
Br |
|
|
|
|
|
|
|
| 36 |
Kr |
|
|
|
|
|
|
|
| 37 |
Ru |
|
|
|
|
|
|
|
| 38 |
Sr |
|
|
|
|
|
|
|
| 39 |
Y |
|
|
|
|
|
|
|
| 40 |
Zr |
|
|
|
|
|
|
|
| 41 |
Nb |
|
|
|
|
|
|
|
| 42 |
Mo |
|
|
|
|
|
|
|
| 43 |
Tc |
|
|
|
|
|
|
|
| 44 |
Ru
|
|
|
|
|
|
|
|
| 45 |
Rh |
|
|
|
|
|
|
|
| 46 |
Pd |
|
|
|
|
|
|
|
| 47 |
Ag |
|
|
|
|
|
|
|
| 48 |
Cd |
|
|
|
|
|
|
|
| 49 |
In |
|
|
|
|
|
|
|
| 50 |
Sn |
|
|
|
|
|
|
|
| 51 |
Sb |
|
|
|
|
|
|
|
| 52 |
Te |
|
|
|
|
|
|
|
| 53 |
I |
|
|
|
|
|
|
|
| 54 |
Xe |
|
|
|
|
|
|
|
| 55 |
Cs |
|
|
|
|
|
|
|
| 56 |
Ba |
|
|
|
|
|
|
|
| 57 |
La |
|
|
|
|
|
|
|
| 58 |
Ce |
|
|
|
|
|
|
|
| 59 |
Pr |
|
|
|
|
|
|
|
| 60 |
Nd |
|
|
|
|
|
|
|
| 61 |
Pm |
|
|
|
|
|
|
|
| 62 |
Sm |
|
|
|
|
|
|
|
| 63 |
Eu |
|
|
|
|
|
|
|
| 64 |
Gd |
|
|
|
|
|
|
|
| 65 |
Tb |
|
|
|
|
|
|
|
| 66 |
Dy |
|
|
|
|
|
|
|
| 67 |
Ho |
|
|
|
|
|
|
|
68
|
Er |
|
|
|
|
|
|
|
69
|
Tm |
|
|
|
|
|
|
|
70
|
Yb |
|
|
|
|
|
|
|
71
|
Lu |
|
|
|
|
|
|
|
72
|
Hf |
|
|
|
|
|
|
|
73
|
Ta |
|
|
|
|
|
|
|
74
|
W |
|
|
|
|
|
|
|
75
|
Re |
|
|
|
|
|
|
|
76
|
Os |
|
|
|
|
|
|
|
77
|
Ir |
|
|
|
|
|
|
|
78
|
Pt |
|
|
|
|
|
|
|
79
|
Au |
|
|
|
88 nm |
|
540 nm |
|
80
|
Hg |
|
|
|
|
|
|
|
81
|
Tl |
|
|
|
|
|
|
|
82
|
Pb |
|
|
|
|
|
|
|
83
|
Bi |
|
|
|
|
|
|
|
84
|
Po |
|
|
|
|
|
|
|
85
|
At |
|
|
|
|
|
|
|
86
|
Rn |
|
|
|
|
|
|
|
87
|
Fr |
|
|
|
|
|
|
|
88
|
Ra |
|
|
|
|
|
|
|
89
|
Ac |
|
|
|
|
|
|
|
90
|
Th |
|
|
|
|
|
|
|
| 91 |
Pa |
|
|
|
|
|
|
|
| 92 |
U |
|
|
|
|
|
|
|
| Reference |
|
|
|
|
|
|
|
[1] H. Bethe, Handbook of Physics, Springer, Berlin Heidelberg New York, 1933.
[2] K. Kanaya, S. Okayama, J. Phys. D., J. Appl. Phys. 1972, 5, 43.
|