=================================================================================
In crystals, a periodic potential appears because the ions are arranged with a periodicity of their Bravais lattice. The periodic potential can be given by,
U(r + R) = U(r) ----------------------------------- [2204a]
where,
R -- The lattice vector.
This potential can be applied into the Schrödinger equation,
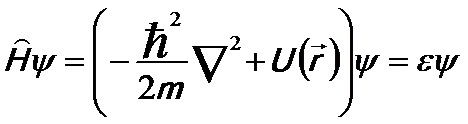 ------------------- [2204b] ------------------- [2204b]
The eigenstates ψ of the Hamitonian Ĥ in Equation 2204b can be chosen to have the form of a plane wave times a function with the periodicity of the Bravais lattice so that each eigenstate ψ satisfies,
ψnk(r) = eik•runk(r) ------------------- [2204c]
where,
ħk is the crystal momentum (but not true momentum);
n -- The quantum number (also called the band index, are equal to 1, 2, 3, . . .);
unk(r + R) = unk(r) -------------------- [2204d]
The quantum number (n) corresponds to the appearance of independent eigenstates of different energies but with the same k. Equation 2204d means that unk(r) has the same periodicity as the Hamitonian Ĥ for any lattice vector R of the Hamitonian.
An alternative formulation of Bloch’s theorem is that the eigenstates of a periodic Hamitonian Ĥ can be chosen so that for any lattice vector R of the Hamitonian, associated with each ψ is a wave vector k and thus each eigenstate satisfies,
ψnk(r+R) = eik•Rψnk(r) ------------------- [2204e]
|
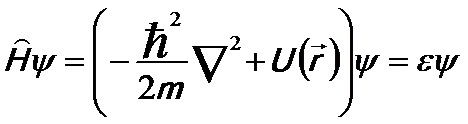 ------------------- [2204b]
------------------- [2204b]