=================================================================================
The elements with larger atomic number (Z) has stronger elastic and thermal diffuse scattering and thus, a solid composed of element with larger Z can have larger mean free path value λ, i.e. weaker inelastic scattering. In the measurements of electron diffractions in TEM, the contribution of inelastically scattered electrons increases with decreasing atomic number and increasing foil thickness.
The fraction F of electron scattering (including both elastic and inelastic scatterings) at angles smaller than a scattering angle β can be given by, [1]
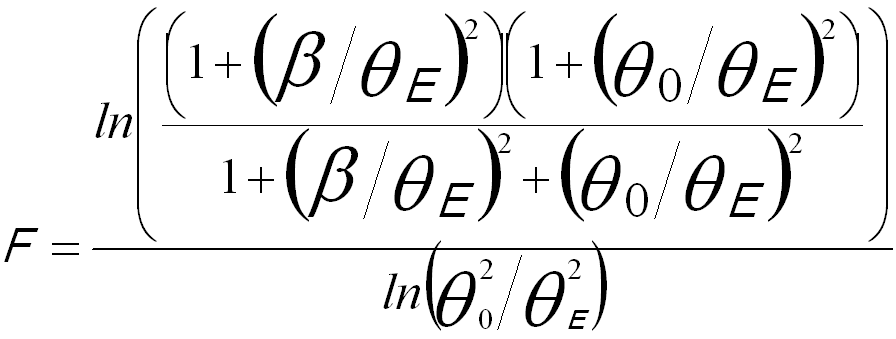 --------------------------------- [3504a] --------------------------------- [3504a]
where,
θ0 -- (≈λZ1/3/(2πa0)) The soft cutoff to the Lorentzian angular distribution,
θE ≈ 0.5Em/E0 (non-relativistically)
Figure 3504a shows the experimental values of λel [2] and λin(Z) [3] as oscillatory functions of Z for Z > 20. Comparison of λel and λin values suggests that the elastic component should dominate scattering of incident high-energy electrons for most inorganic solids and of incident electrons penetrating thin TEM specimens.
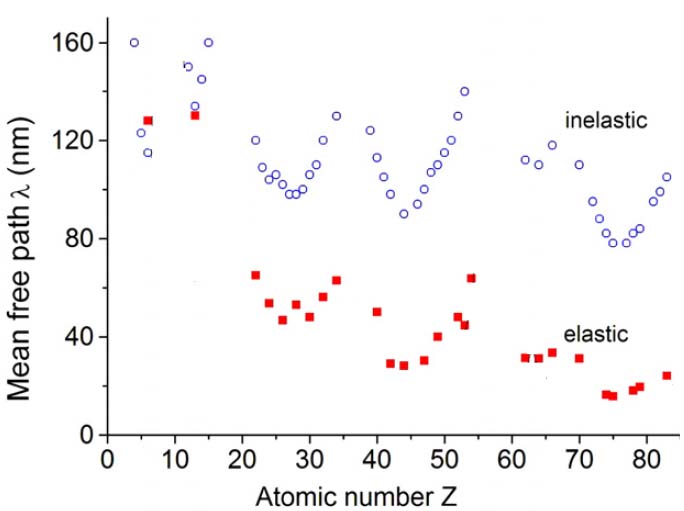
Figure 3504a. The mean free path of elastic scattering λel of 200 keV electrons (solid squares) [2] and that of inelastic values λin (open circles) (Adapted from [3]).
In general, the higher the effective atomic number, the higher is
the inelastic differential cross-section. However, the ratio of the
inelastic to the elastic scattering cross-section is inversely
proportional to the effective atomic number, [4]
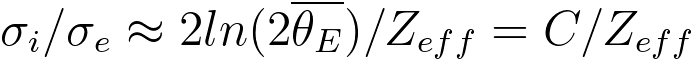 ------------------------ [3504b] ------------------------ [3504b]
where,
σi --
the inelastic scattering cross-section,
σe --
the elastic scattering cross-section,
Zeff -- the effective atomic number,
C -- a coefficient,
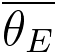 -- the characteristic angle corresponding to the mean energy loss. -- the characteristic angle corresponding to the mean energy loss.
Figure 3504b shows the angle at which inelastic and elastic differential cross-sections are equal, as a function of the atomic number Z at the energy loss of 10 eV.
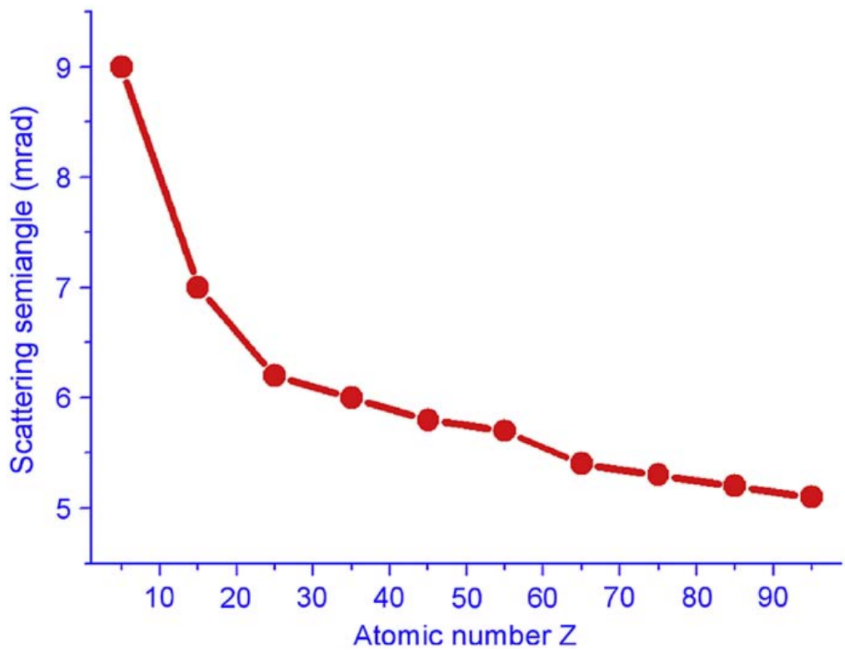
| Figure 3504b. Plot of the scattering angle at which elastic and inelastic differential cross-sections are equal, as a function of the atomic number at an energy loss of 10 eV. [5] |
[1] F. Lenz, Z. Naturforsh 9A (1954) 185.
[2] Konstantin Iakoubovskii and Kazutaka Mitsuishi, Elastic scattering of 200 keV electrons in elemental solids: experimental observation of atomic-number-dependent oscillatory behavior, J. Phys.: Condens. Matter 21 (2009) 155402.
[3] Iakoubovskii K, Mitsuishi K, Nakayama Y and Furuya K (2008) Phys. Rev. B 77, 104102.
[4] A.V. Crewe, J.P. Langmore, M.S. Isaacson, Physical aspects of electron microscopy and microbeam analysis, in: B.M. Siegel, D.R. Beaman (Eds.),
Wiley, New York, 1975, p. 47.
[5] Lin Gu, Wilfried Sigle, Christoph T. Koch, Jaysen Nelayah, Vesna Srot, Peter A. van Aken, Mapping of valence energy losses via energy-filtered annular dark-field scanning transmission electron microscopy, Ultramicroscopy 109 (2009) 1164–1170.
|