=================================================================================
If all of the atoms in a crystal are the same size, the maximum number of atoms that are coordinated around any individual is 12 (also called 12-fold coordination) in which there are two ways that atoms can be packed. For a single layer of atoms with an equal size, there are two kinds of voids between the atoms as shown in Figure 3547a (a):
i) B voids with triangles pointing up.
ii) C voids with the triangles pointing down.
As shown in Figure 3547a (b), if the second layer of atoms is added and its atoms occupy the space above the B voids and the third layer of atoms is added and its atoms occupy the positions over the C voids in the A layer, this will result in cubic closest packing with a stacking sequence of ABC ABC ABC.... etc.
Figure 3547a. Formation of cubic closest packing: (a) Single layer of atoms, and (b) Formed cubic closest packing structure.
According to Radius Ratio Rule, the limiting cation-to-anion radius ratios for cubic ionic lattices can be obtained as shown in Table 3547a.
Table 3547a. Cation-to-anion radius ratios (r+/r-) for coordination numbers (CN) 12 and 8.
|
CN |
Crystal type |
Geometric shape |
Material examples and their r+/r- |
1.0 |
12 |
Hexagonal or cubic
closest packing |
|
Metals |
| 0.732 - 1.0 |
8 |
Cubic |
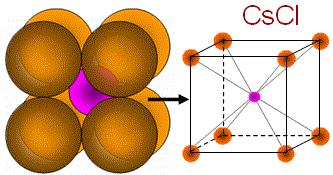 |
(i) Binary AB: CsCl (1.13), KCl (0.91), CsBr (0.862); (ii) Binary AB2: CaF2 (0.727); (iii) Others: NH4Br |
Close-packing of equal spheres (e.g. the same atoms in a crystal) can form the trigonal, hexagonal or cubic crystal systems. The structure belongs to the trigonal system if the structure has the minimum symmetry, while it belongs to the hexagonal system if it has a 63 axis of symmetry.
Table 3547b and Figure 3547b show the cubic crystal systems and the schematic illustrations of the cubic lattices, respectively.
Table 3547b. Cubic crystal systems.
Crystal
family |
Crystal
system |
Required
symmetries
of point group |
Point
group |
Space
group |
Bravais
lattices |
Lattice
system |
Cubic
|
4 three-fold axes of rotation |
5 |
36 |
3 |
Cubic |

Figure 3547b. Schematic illustrations of the Bravais lattices of cubic crystals. Table 3547c. Relationship between Laue classes and point groups.
System |
Essential symmetry |
|
|
|
| |
None |
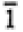 |
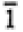 |
1, -1 |
| |
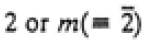 |
2/m |
2/m |
2, m, 2/m |
| |
222 or 2mm
|
mmm
|
mmm |
222, mm2, mmm |
| |
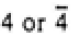 |
4/mmm
|
4/m
|
4, -4, 4/m |
| 4/mmm |
422, -42m, 4mm, 4/mmm |
|
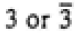 |
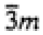 |
3 |
3, -3 |
| -3m1 |
321, 3m1, -3m1 |
| -31m |
312, 31m, -31m |
|
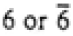 |
6/mmm
|
6/m |
6, -6, 6/m |
| 6/mmm |
622, -62m, 6mm, 6/mmm |
Cubic |
23 |
m3m
|
m-3 |
23, m-3 |
| m-3m |
432, -43m, m-3m |
Table 3547d lists the characteristics of the three cubic Bravais lattices.
Table 3547d. The only three cubic Bravais lattices.
Lattice |
Number of
lattice points
per unit cell |
Number of
atoms
per unit cell |
Nearest distance
between lattice points |
Maximum packing |
Maximum packing condition |
Density (or fraction of packing, Vatom/Vcell) |
|
1 |
1 |
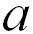 |
When the adjacent atoms touch each other along the edge
of the cube |
52.4% |
|
2 |
2 |
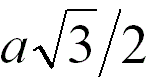 |
When the adjacent atoms touch each other along
the body diagonal of the cubic cell |
68.0% |
|
4 |
4 |
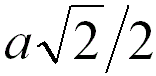 |
When the adjacent atoms touch each other along
the face diagonal of the cubic cell |
74.0% |
|
4 |
8 |
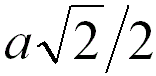 |
|
34 % |
Table 3547e. Some symmetrical diffraction patterns of cubic crystals.
Zone axis |
[100] |
[110] |
[111] |
Symmetry |
Square |
Rectangular |
Hexagonal |
Aspect Ratio |
1:1 |
1: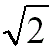 for BCC, SC (almost hexagonal for FCC) for BCC, SC (almost hexagonal for FCC) |
Equilateral |
Cubic lattices have the highest degree of symmetry of any Bravais lattices.
The lattice spacing of cubic structures may be given by, (You can download the excel file for your own calculations)
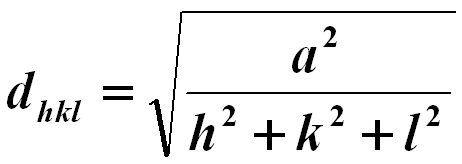 ------------------------------- [3547a] ------------------------------- [3547a]
where,
a -- The lattice constant.
hkl -- The Miller indices.
The interfacial angles of cubic crystals can be given by,
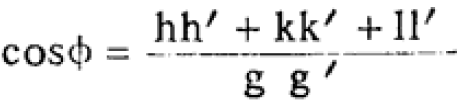 ------------------------ [3547b] ------------------------ [3547b]
Using Equation 3547b, we can obtain Table 3547f.
Table 3547f. Interfacial angles of cubic crystals between {h k l} and {h' k' l'} planes.
| |
{h k l} |
| {h' k' l'} |
100 |
110 |
111 |
210 |
211 |
221 |
310 |
| 100 |
0
90.0 |
|
|
|
|
|
|
| 110 |
45.0
90.0 |
0
60.0
90.0 |
|
|
|
|
|
| 111 |
54.7 |
35.3
90.0 |
0
70.5
109.5 |
|
|
|
|
| 210 |
26.5
63.4
90.0 |
18.4
50.8
71.6 |
39.2
75.0 |
0
36.9
53.1 |
|
|
|
| 211 |
35.3
65.9 |
30.0
54.7
73.2
90.0 |
19.5
61.9
90.0 |
24.1
43.1
56.8 |
0
33.6
48.2 |
|
|
| 221 |
48.2
70.5 |
19.5
45.0
76.4
90.0 |
15.8
54.7
78.9 |
26.6
41.8
53.4 |
17.7
35.3
47.1 |
0
27.3
38.9 |
|
| 310 |
18.4
71.6
90.0 |
26.6
47.9
63.4
77.1 |
43.1
68.6 |
8.1
32.0
45.0 |
25.4
40.2
58.9 |
32.5
42.5
58.2 |
0
25.9
36.9 |
| 311 |
25.2
72.5 |
31.5
64.8
90.0 |
29.5
58.5
80.0 |
19.3
47.6
66.1 |
10.0
42.4
60.5 |
25.2
45.3
59.8 |
17.6
40.3
55.1 |
| 320 |
33.7
56.3
90.0 |
11.3
54.0
66.9 |
36.8
80.8 |
|
|
|
|
| 321 |
36.7
57.7
74.5 |
19.1
40.9
55.5 |
22.2
51.9
72.0
90.0 |
|
|
|
|
| 331 |
46.5 |
13.1 |
22.0 |
|
|
|
|
| 510 |
11.4 |
|
|
|
|
|
|
In crystals, anisotropy of many properties clearly arises because the arrangement of their atoms varies in different directions. In general, cubic crystals is less anisotropic than monoclinic ones because of their greater symmetry, for instance, with respect to electrical conductivity. Therefore, cubic crystals do not exhibit electrical polarization when the temperature is changed, so that their pyroelectric effect is isotropic.
Table 3547g. Other characteristics of cubic structures.
Contents |
Page |
| Angles in unit cells |
page3555 |
| Volume of unit cells |
page3033 |
| Bravais lattices |
page4546 |
| Relationship between three-dimensional crystal families, crystal systems, space group, point group, lattice systems and symmetries |
page4549 |
|

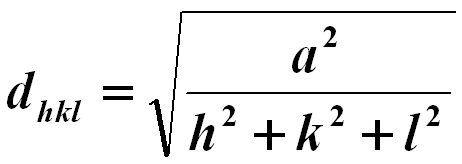 ------------------------------- [3547a]
------------------------------- [3547a] 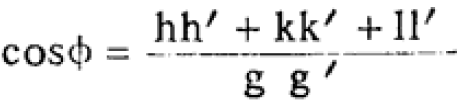 ------------------------ [3547b]
------------------------ [3547b]