|
This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
|
=================================================================================
Under axial illumination conditions it is not possible to measure all aberration coefficients. In this case, only the defocus and the twofold astigmatism can be determined by the defocus-based techniques. The other aberration coefficients, e.g. spherical aberration, need to be provided by the microscope manufacturer or to be determined by different methods. However, those aberration coefficients, such as the axial coma and the threefold astigmatism, cannot be ignored at high spatial resolutions approaching 0.1 nm. Therefore, the measurements of the other aberration coefficients should be done by other methods such as tilting the illumination. Note that we need to realize that tilting illumination also changes the defocus, astigmatism, and the original aberrations.
Figure 3676a shows the simulated intensity distribution patterns of 200 keV-electron probes at 100 nm of B2 (second-order axial coma), 100 nm of A2 (three-fold axial astigmatism), 1 µm of S3 (axial star aberration of the 3rd order), and 2 µm of A3 (four-fold axial astigmatism).
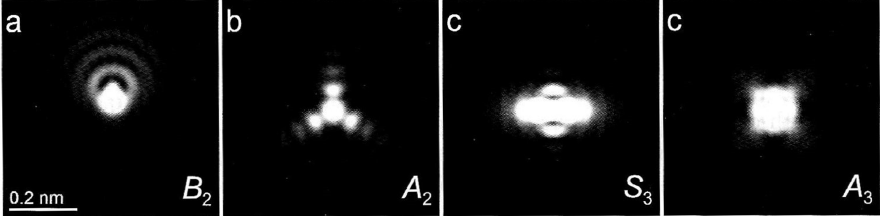
Figure 3676a. Simulated intensity distribution patterns of 200 keV-electron probes: (a) B2 = 100 nm, (b) A2 = 100 nm, (c) S3 = 1 µm, and (d) A3 = 2 µm. In this simulation, the defocus C1 was set to -3 nm, the imaginary parts of the aberrations to zero, and the illumination semi-angle to 30 mrad. [1]
Figure 3676b shows the schematic comparison of Zemlin (diffractogram)-tableau characteristics for the axial aberrations up to third orders. First-order aberration (e.g. defocus and twofold astigmatism, A1) shows the elliptical distortion even without electron beam tilting because the impact of first-order aberrations does not depend on the tilt angle. For the aberrations of higher orders (n≥2), such as second-order axial coma B2, three-fold astigmatism A2, third-order spherical aberration C3 (>0), third-order star aberration S3 and four-fold astigmatism A3, there is no elliptical distortion observable for the un-tilted case. In these cases, only at illumination tilts the characteristic distortion due to the aberrations becomes discernible. Note that the higher-order aberrations have equal symmetries to the ones in Figure 3676b as discussed in page3740.
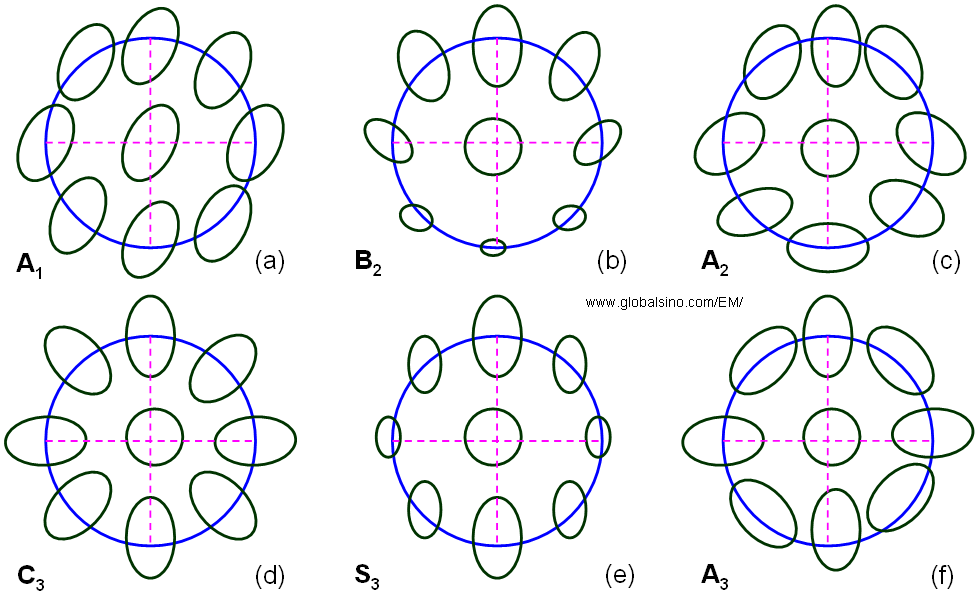
Figure 3676b. Schematic representation of Zemlin (diffractogram)-tableau characteristics for the axial aberrations up to third order.
[1] Simulation of Rolf Erni.
|

