=================================================================================
The periodic potential in crystals causes the amplitude of the accelerating electron (e.g. 200 keV in TEM) to be transferred back-and-forth between the transmitted and diffracted wavefunctions. This transfer process can be explained by dynamical theory. The crystal has a periodic potential that is weak compared with an electron energy of 200 keV. At the Laue condition ( s= 0), the physical distance between two back-and-forth transfers is called the “extinction distance.”
Assuming the TEM specimen is a perfect crystal, in two beam condition the intensity (Ig) of diffracted electron beam can be given by (based on dynamical theory),
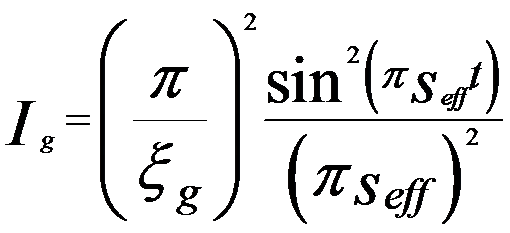 ------------------------- [4134a] ------------------------- [4134a]
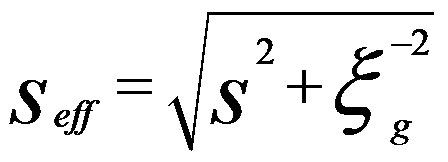 ------------------------- [4134b] ------------------------- [4134b]
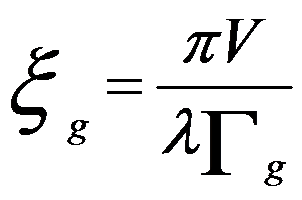 ------------------------- [4134c] ------------------------- [4134c]
where,
seff -- Effective deviation parameter
ξg -- Extinction distance
V -- Volume of the unit cell
λ -- Electron wavelength
Γg -- Structure factor of the unit cell for diffraction g
s -- Deviation parameter
t -- Crystal thickness
Equation 4134a for dynamical theory is valid when the TEM sample is thick and s is about zero, but is not valid in kinematical theory. From Equation 4134c we can know that the extinction distance decreases with increase of scattering (increase of Γg). When s is equal to zero (exact Bragg condition) we have seff = 1/ξg, meaning the transmitted (I0) and diffracted (Ig) intensities has a periodicity of ξg in TEM specimen depth indicated in Figure 4134 in two beam condition. Here, I0 = 1 - Ig in two beam condition. Equation 4134a also indicates that the intensity of these low order diffraction disks
fluctuates with thickness.
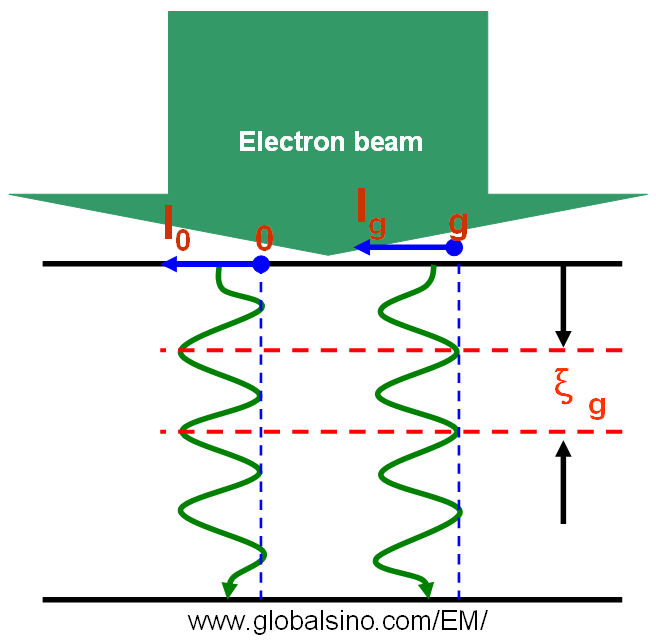
Figure 4134. The diffracted intensity (Ig) showing a periodicity of ξg in TEM
specimen depth in two beam condition. Ig is the intensity of transmitted beam.
|