=================================================================================
The magnification of electron microscopes is defined as the ratio of a specimen size and an image size recorded on a CCD camera or photo-film.
As discussed in Bell-Shaped Field in EMs, by introducing dimensionless coordinates y = r/a and x = z/a = cot φ (where we have the variable φ varying from π (z = −∞) to π/2 (z = 0) and then to 0 (z = +∞).), by following the theory of trajectories of electron in electron lenses,
and by assuming a ray passing through a point P0(y0, φ0) in front of the lens, a image point P1(y1, φ1) can be theoretically obtained,
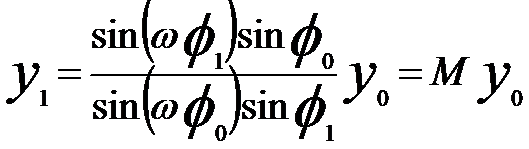 -------------------------- [4274a] -------------------------- [4274a]
where,
M -- Magnification
ω -- Lens strength, given by,
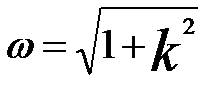 ---------------------------------- [4274b] ---------------------------------- [4274b]
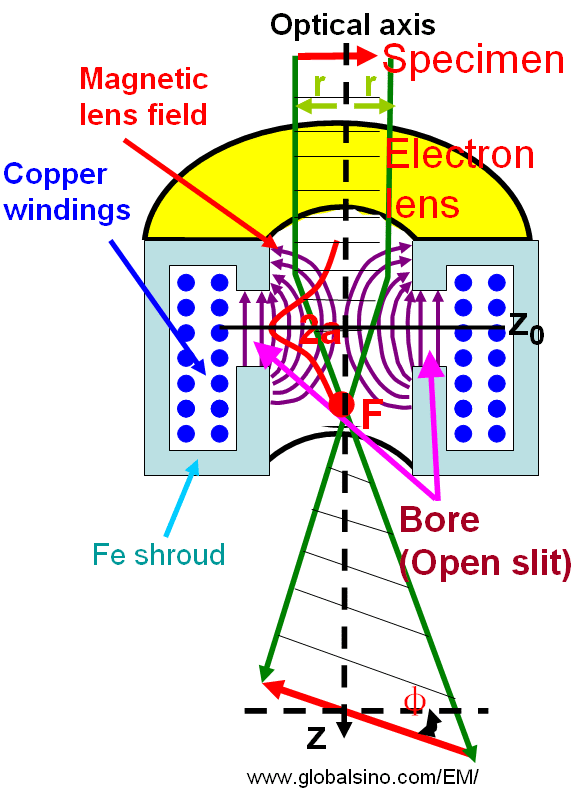
Figure 4274. Rotationally symmetric magnetic fields and electron lenses.
Newton’s lens equation of light optics suggests Z0Z1 = f0f1. Further calculation based on bell-shaped field, we can obtain,
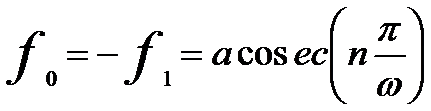 -------------------------- [4274c] -------------------------- [4274c]
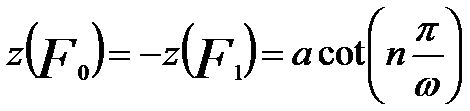 ------------------- [4274d] ------------------- [4274d]
We can see that the focal lengths f0 and f1 are not the same as the distances z(F0) and z(F1) of the foci from the lens center at z = 0, indicating that electron lenses cannot be treated as thin lenses.
The magnification M in Equation 4274a can be re-written in terms of f and Z,
M = f0/Z0 = Z1/f1 ------------------- [4274e]
|
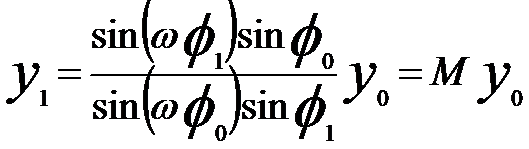 -------------------------- [4274a]
-------------------------- [4274a]
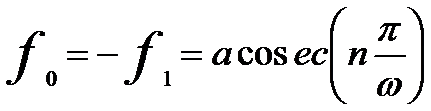 -------------------------- [4274c]
-------------------------- [4274c]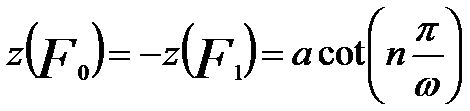 ------------------- [4274d]
------------------- [4274d]