Seven Crystal Families
- Practical Electron Microscopy and Database -
- An Online Book -

https://www.globalsino.com/EM/  



 

This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.

 

=================================================================================

Space groups represent the ways that the macroscopic and microscopic symmetry elements (operations) can be self-consistently arranged in space. There are totally 230 space groups. The space groups add the centering information and microscopic elements to the point groups. Depending on their geometry, crystals are commonly classified into seven systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal and cubic. Figure 4548a schematically shows the relationship between the 7 crystal systems, 14 Bravais Lattices, 32 point groups, and 230 space groups. Table 4548a also lists the relation between three-dimensional crystal families, crystal systems, and lattice systems. Table 4548b also shows the seven crystal systems and the restrictions on their cell dimensions (cell edges and cell angles).

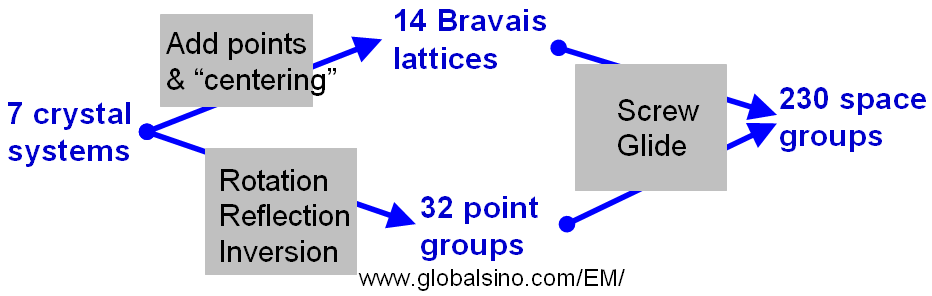
The relationship between the 7 crystal systems, 14 Bravais Lattices, 32 point groups, and 230 space groups

Figure 4548a. The relationship between the 7 crystal systems,
14 Bravais Lattices, 32 point groups, and 230 space groups.

Table 4548a. The relation between three-dimensional crystal families, crystal systems, and lattice systems.

Crystal
family		 Crystal
system		 Required
symmetries
of point group		 Point
group		 Space
group		 Bravais
lattices		 Lattice
system
Triclinic None 2 2 1 Triclinic
Monoclinic
1 two-fold axis of rotation or 1 mirror plane 3
 13
 2
 Monoclinic

Orthorhombic

3 two-fold axes of rotation or 1 two-fold axis of rotation and two mirror planes 3 59 4
Orthorhombic

Tetragonal

1 four-fold axis of rotation

7

68

2

 Tetragonal
Hexagonal Trigonal 1 three-fold axis of rotation 5 7 1 Rhombohedral
18 1 Hexagonal
Hexagonal 1 six-fold axis of rotation 7 27
Cubic
 4 three-fold axes of rotation 5 36 3 Cubic
Total: 6 7   32 230 14 7

As indicated in Table 4548a, the 14 basic Bravais lattice types give rise to a total of 230 possible crystal types when they are combined with other symmetry operators such as mirrors planes, glide planes, and screw axes.

Table 4548b. The seven crystal systems (families) and the restrictions on their cell dimensions.

Crystal family Cell edges Cell angles
Triclinic None None
Monoclinic None α = γ = 90°
Orthorhombic None α = β = γ = 90°
Tetragonal a = b α = β = γ = 90°
Trigonal, hexagonal a = b α = β = 90°, γ = 120°
Cubic a = b = c α = β = γ = 90°

Figure 4548b shows the schematic illustration of the different classes of crystal systems and their properties.

No center of symmetry (21 point groups)
Center of symmetry (11 point groups)
 
Non-piezoelectric (1 point groups)
 
Non-pyroelectric
 
Ferroelectric (Only if polarization Is reversible)
Non-ferroelectric

Figure 4548b. Schematic illustration of the different classes of crystal systems and their properties.

 

 
=================================================================================

The book author (Yougui Liao) welcomes your comments, suggestions, and corrections, please click here for submission. If you let book author know once you have cited this book, the brief information of your publication will appear on the “Times Cited” page.