=================================================================================
Space groups represent the ways that the macroscopic and microscopic symmetry elements (operations) can be self-consistently arranged in space. There are totally 230 space groups. The space groups add the centering information and microscopic elements to the point groups. Figure 4549a schematically shows the relationship between the 7 crystal systems, 14 Bravais Lattices, 32 point groups, and 230 space groups. The seven holohedric point groups F0 and all their subgroups (merohedral groups) form the 32 crystallographic point groups.
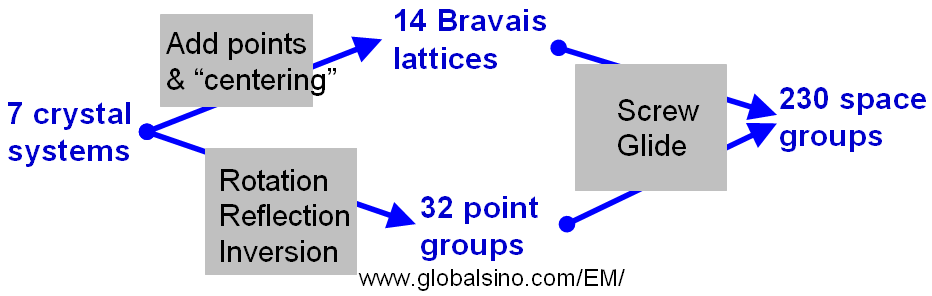
Figure 4549a. The relationship between the 7 crystal systems,
14 Bravais Lattices, 32 point groups, and 230 space groups.
Nicolaus Steno first showed in 1669 that the angles between the faces of crystals are constant, independently of the regularity of a given crystal morphology. The analysis of crystal morphologies led to the formulation of a complete set of 32 symmetry classes, called “point groups” as shown in Table 4549a. The morphologies of all crystals obey the 32 point groups. Possible symmetry elements are 1-, 2-, 3-, 4-, and 6-fold rotations, mirror plane m, inversion center and a combination of rotation axis with inversion center (inversion axis). Table 4549b shows the relation between three-dimensional crystal families, crystal systems, and lattice systems. 32 point groups indicate that there are only 32 possible combinations of symmetry elements. Furthermore, Table 4549c lists the symmetry groups for the crystal systems together with the point groups with Hermann–Mauguin notation.
Table 4549a. 32 point groups (Notation: Schönflies).

Table 4549b. The relation between three-dimensional crystal families, crystal systems, and lattice systems.
Crystal
family |
Crystal
system |
Essential
symmetries
of point group |
Point
group |
Space
group |
Bravais
lattices |
Lattice
system |
Triclinic |
1-fold axis |
2 |
2 |
1 |
Triclinic |
Monoclinic
|
1 two-fold axis (parallel to y) of rotation or 1 mirror plane |
3
|
13
|
2
|
Monoclinic |
Orthorhombic |
3 two-fold axes of rotation or 1 two-fold axis of rotation and two mirror planes |
3 |
59 |
4 |
Orthorhombic |
Tetragonal |
1 four-fold axis (parallel to z) of rotation |
7 |
68 |
2 |
Tetragonal |
Hexagonal |
Trigonal |
1 three-fold axis (parallel to z) of rotation |
5 |
7 |
1 |
Rhombohedral |
| 18 |
1 |
Hexagonal |
Hexagonal |
1 six-fold axis (parallel to z) of rotation |
7 |
27 |
Cubic
|
4 three-fold axes of rotation |
5 |
36 |
3 |
Cubic |
Total: 6 |
7 |
|
32 |
230 |
14 |
7 |
Table 4549c. Symmetry groups for the crystal systems.
System |
Essential symmetry |
Lattice symmetry |
Diffraction (Laue) symmetry |
Point Groups (Hermann–Mauguin notation) |
X |
|
X⊥m
(X/m) |
X||m (Xm) |
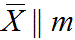 ( 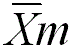 ) |
X⊥2 |
X⊥m||m |
| |
None |
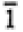 |
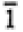 |
1 |
-1 |
-- |
-- |
-- |
-- |
-- |
| |
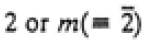 |
2/m |
2/m |
2 |
m |
2/m |
-- |
-- |
-- |
-- |
| |
222 or 2mm
|
mmm
|
mmm |
-- |
-- |
-- |
mm2 |
-- |
222 |
mmm |
| |
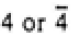 |
4/mmm
|
4/m
|
4 |
-4 |
4/m |
-- |
-- |
-- |
-- |
| 4/mmm |
-- |
-- |
-- |
4mm |
42m |
422 |
4/mmm |
|
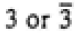 |
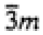 |
3 |
3 |
-3 |
-- |
-- |
-- |
-- |
-- |
| -3m1 |
-- |
-- |
-- |
3m |
-3m1 |
321 |
-- |
| -31m |
-- |
-- |
-- |
-31m |
312 |
-- |
|
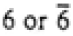 |
6/mmm
|
6/m |
6 |
-6 |
6/m |
-- |
-- |
-- |
-- |
| 6/mmm |
-- |
-- |
-- |
6mm |
-62m |
622 |
6/mmm |
|
23 |
m3m
|
m-3 |
23 |
m-3 |
-- |
-- |
-- |
-- |
-- |
| m-3m |
-- |
-- |
-- |
-- |
4-3m |
432 |
m-3m |
*
X: Major X-fold rotation axis alone.
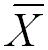 : Inversion axis alone, namely, the major X-fold inversion axes.
X/m: Rotation axis with a symmetry plane normal to it.
Xm: Rotation axis with a symmetry plane that is not normal to it (usually a vertical symmetry plane).
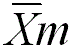 : Inversion axis with a symmetry plane not normal to it.
X⊥2: Rotation axis with a diad normal to it (The two-fold rotation axis is perpendicular to the major axis).
X/mm: Rotation axis with a symmetry plane normal to it and another not so. |
Of the 32 point groups, 11 crystal classes are centrosymmetric and thus possess no polar properties. Of the remaining 21 non-centrosymmetric classes, 20 classes show electrical polarity when a stress is applied.
Figure 4549b shows the schematic illustration of the different classes of crystal systems and their properties. In ferroelectric substances, the number of distinct spontaneous polarization directions depends on its point group symmetry.
|
|
32 point groups |
|
|
|
|
|
|
|
|
|
|
|
|
|
Non-pyroelectric |
|
|
|
|
Non-ferroelectric |
Figure 4549b. Schematic illustration of the different classes of crystal systems and their properties.
|