=================================================================================

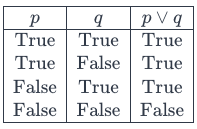
Proposition symbols are a fundamental concept in propositional logic, a branch of logic that deals with propositions and their logical relationships. They provide a way to express and manipulate statements in a formal, systematic manner.  In logic, a proposition is a statement that is either true or false, but not both. Proposition symbols, also known as propositional variables or propositional letters, are placeholders for such statements. 

They are typically represented by letters from the alphabet, often p, q, r,…. For instance, if p represents the proposition "It is raining," then q might represent "The ground is wet." We can then form compound propositions by combining these symbols using logical connectives such as AND (∧), OR (∨), NOT (¬), implication (→), biconditional (↔), etc.  For AND, OR, and NOT, we have:
   
   
   

The implication connective represents "if...then" statements. In symbolic logic, if p is a proposition, and q is another proposition, then p→q means "if p, then q." The truth table for implication is such that it is false only when the antecedent (p) is true and the consequent (q) is false. The truth table is as follows: 

In Python, we can use p -> q or not p or q to represent implication. 

The biconditional connective represents "if and only if" statements. In symbolic logic, if p is a proposition, and q is another proposition, then p↔q means "p if and only if q." The truth table for the biconditional is true when both propositions have the same truth value. The truth table is as follows: 

    
In Python, we can use p <-> q or (p and q) or (not p and not q) to represent the biconditional.

With the example above, then we have:

     p∧q represents "It is raining and the ground is wet." 

     p∨q represents "It is either raining or the ground is wet."

     ¬p represents "It is not raining."

A simple Python script that illustrates the use of proposition symbols and logical operations is shown below. 

    
Then, the output is:
    

The script defines two proposition symbols, p and q, and then demonstrates various logical operations using these symbols.

Another script example is: 

     
Output:
     

============================================