=================================================================================
Sigmoid, hyperbolic tangent (tanh), and rectified linear unit (ReLU) are activation functions commonly used in artificial neural networks. Table 3730 lists the comparison among them.
Table 3730. Comparison among sigmoid, hyperbolic tangent (tanh) and rectified linear unit (ReLU) functions.
| |
Sigmoid |
Tanh |
ReLU |
| Plot |
 |
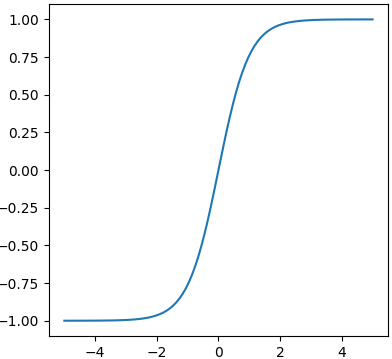 |
 |
|
| Formula |
|
|
|
| Range of Output |
Outputs values between 0 and 1, which can be interpreted as probabilities. |
Outputs values between -1 and 1, which can help mitigate issues with the vanishing gradient problem compared to sigmoid. |
Outputs values in the range [0, +∞). Negative inputs result in zero, while positive inputs are passed through. |
| Vanishing Gradient |
Prone to the vanishing gradient problem, especially for extreme values, which can slow down or prevent learning in deep networks. That is, for very large positive and very low values of x, the slope (derivative) becomes very close to zero. |
Less prone to vanishing gradients compared to sigmoid, but still has some susceptibility. |
Generally doesn't suffer from the vanishing gradient problem for positive values, making it well-suited for deep networks. |
| Computational Efficiency |
Computationally more expensive compared to ReLU, especially during training, as exponentials are involved. |
Simple and computationally efficient, involving only a simple threshold operation. |
| Sparsity |
Outputs are not sparse, meaning a significant portion of the values are non-zero. |
Can induce sparsity since all negative values are set to zero. |
| Activation Sparsity |
The activations are not sparse, meaning many neurons may be activated simultaneously. |
Can lead to sparse activation because some neurons may not activate for certain inputs. |
| Dead Neurons |
Prone to the "dying ReLU" problem where neurons may become inactive and stop learning. |
Susceptible to dead neurons, where neurons may become inactive for all inputs with a negative output. |
| Implementation |
Used in the hidden layers of networks where the data ranges from -1 to 1 or 0 to 1. |
Commonly used in hidden layers, but may cause issues for certain types of data (e.g., all negative values). |
| Advantages |
Smooth Gradients:
Sigmoid has smooth gradients, which can be advantageous for optimization algorithms that rely on gradient information, such as gradient descent. This smoothness facilitates stable convergence during training.
Clear Interpretation:
The output of the sigmoid function can be interpreted as probabilities, mapping values to the range (0, 1). This is useful in binary classification problems where the output can be treated as the probability of belonging to a particular class. |
Zero-Centered Output:
The tanh function outputs values in the range [-1, 1], with the center at 0. This zero-centered property can be advantageous for optimization, as it helps mitigate issues like the vanishing gradient problem that are associated with functions like the sigmoid.
Smooth Gradients:
Like the sigmoid, tanh has smooth gradients, which can be beneficial during optimization using gradient-based methods. Smooth gradients make it easier for optimization algorithms to find the minimum of the loss function.
Clear Interpretation:
Similar to the sigmoid, tanh has a clear interpretation, mapping inputs to values in the range of probabilities. This can be useful in scenarios where a probabilistic interpretation is desired.
Mitigation of Exploding Gradients:
Tanh can help mitigate the exploding gradient problem better than sigmoid, as its output range is [-1, 1]. This can be particularly useful in deep networks. |
Computational Efficiency:
ReLU is computationally efficient, involving only a threshold operation where negative values are set to zero. This simplicity makes it faster to compute compared to functions involving exponentials, like sigmoid and tanh.
Avoidance of Vanishing Gradient:
ReLU is less prone to the vanishing gradient problem for positive values. This can be especially advantageous in deep networks, where maintaining non-zero gradients for weight updates is crucial for learning.
Sparse Activation:
ReLU can induce sparsity in the network activations, as neurons with negative outputs become inactive. Sparse activations can lead to more efficient computation and storage.
Biological Plausibility:
The rectification process in ReLU is more in line with the behavior of real neurons, where they either fire or don't. This biological plausibility can be advantageous in certain contexts, especially when considering neural network architectures inspired by the brain.
Effective for Image Recognition:
ReLU has shown to be particularly effective in convolutional neural networks (CNNs) used for image recognition tasks. The sparsity and computational efficiency of ReLU contribute to its success in these applications. |
Limitations |
Vanishing Gradient:
Sigmoid is prone to the vanishing gradient problem, especially for extreme input values. This can lead to slow or halted learning in deep neural networks as gradients become very small during backpropagation.
Not Zero-Centered:
The sigmoid function is not zero-centered, which means that the average activation of neurons in a layer may shift towards the extremes (0 or 1) during training. This lack of zero-centeredness can complicate weight updates and optimization.
Limited Output Range:
The output of the sigmoid function is in the range (0, 1), which can limit the ability of the network to model complex relationships in the data, especially when the true outputs may have a broader range.
Not Sparse:
Sigmoid outputs are not sparse. In many cases, a large number of neurons may be activated simultaneously, leading to redundancy and potentially increased computational overhead. |
Vanishing Gradient:
Like the sigmoid function, tanh is also susceptible to the vanishing gradient problem, especially for extreme input values. Gradients can become very small during backpropagation, leading to slow or stalled learning in deep networks.
Not Sparse:
Tanh activations are not sparse. Similar to sigmoid, a large number of neurons may be activated simultaneously, potentially leading to redundancy and increased computational overhead.
Output Range:
While tanh addresses the non-zero-centered issue of sigmoid by having outputs in the range [-1, 1], the limited output range can still pose challenges in capturing complex patterns, especially in comparison to activation functions with larger output ranges. |
Dead Neurons:
The "dying ReLU" problem occurs when neurons consistently output zero for all inputs during training. If a large gradient flows through a ReLU neuron, it can update the weights in such a way that the neuron always outputs zero. Once this happens, the neuron becomes inactive and doesn't contribute to the learning process.
Not Zero-Centered:
Similar to the sigmoid function, ReLU is not zero-centered. This lack of zero-centeredness can lead to issues during optimization, as the average activation of neurons may shift towards the positive side.
Exploding Gradient:
ReLU can suffer from the exploding gradient problem, where very large gradients may cause the weights to be updated in such a way that the network becomes unstable and fails to converge.
Not Suitable for All Data Distributions:
ReLU might not perform well on data distributions that have many negative values since all negative inputs result in zero output. This can be addressed by using variants like Leaky ReLU or Parametric ReLU. |
| Common Usage |
Often used in the output layer of binary classification models. |
Commonly used in scenarios where the data has negative values. |
Widely used in hidden layers of deep neural networks, especially in computer vision tasks. |
============================================
|




