=================================================================================

Different from unconditional probability, conditional probability, e.g. P(x₁|x₂), is a concept in probability theory that deals with the probability of an event occurring under a specific condition or given that another event has occurred. That is, it represents the probability of an event x₁ occurring given that another event x₂ has occurred. In other words, it's the probability of x₁ under the condition that x₂ is true.

In machine learning, particularly in probabilistic graphical models or Bayesian statistics, conditional probabilities play a significant role. For example, in Bayesian networks, nodes represent random variables, and the edges between them indicate probabilistic dependencies. The conditional probabilities P(x_i|parents(x_i)) specify how each variable depends on its parents in the graph.

For instance, P(A|B) represents how the probability of one event is affected by the knowledge or occurrence of another event. Conditional probability is denoted as P(A|B), which reads as "the probability of event A occurring given that event B has occurred."

Mathematically, conditional probability is defined as:

          ----------------------------------- [3818a]

Where:

• P(A∣B) is the conditional probability of event A given event B.
• P(A ∩ B), or  P(A and B)  is the probability of both events A and B occurring simultaneously (the joint probability), indicating commutativity of conjunction, which refers to the property of mathematical operations where the order of the operands does not affect the result.
• ∩  represents "AND" or "Λ". 
• P(B) is the probability of event B occurring.

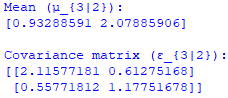
Equivalent Equations of Equation 3818a are:

          P(AΛB) = P(B)P(A|B) -------------------------------- [3818aa]

          P(AΛB) = P(A)P(B|A)   -------------------------------- [3818ab] 

Then, we also can have,

          P(A)P(B|A) = P(B)P(A|B) -------------------------------- [3818ac]

          P(B|A) = P(B)P(A|B)/P(A) -------------------------------- [3818ad]

Equation 3818ad is called Bayes' rule.

For a case of P(X3|X2), then we have,

          ----------------------------------- [3818b]

          ----------- [3818c]

Then, for a conditional distribution of x₃ ​ given x₂​ in a normal distribution, we have,

          ------------------------------------------- [3818d]

          ----------------------- [3818e]

          ----------------------- [3818f]

This code can be used to compute the mean and covariance matrix of the conditional distribution based on Equations 3818e and 3818f, for instance, in the table below.

Table 3818. Computing the mean and covariance matrix of the conditional distribution (code).

Input	Output

Expression 3818d indicates that the conditional distribution of x₃​ given x₂​ is a normal distribution with mean μ_3|2​ and covariance matrix ε_3|2. Equation 3818e is the mean of the conditional distribution, which appears to be a linear combination involving the mean of x₃​(μ₃), the covariance between x₃​ and x₂​(ε_3,2), and the inverse of the covariance of x₂(ε_2,2⁻¹). Equation 3818f is the covariance matrix of the conditional distribution. It involves the covariance of x₃(ε_3,3), the covariance between x₃​ and x₂(ε_3,2), and the inverse of the covariance matrix of x₂(ε_2,2⁻¹). The expressions resemble those found in the multivariate normal distribution, and the use of these equations would typically assume that the joint distribution of x₂​ and x₃​ is multivariate normal.

Some examples about conditional probability are:

1. It's used to update probabilities: Conditional probability allows you to update your knowledge about the probability of an event based on new information. For example, if you know the probability of rain P(A) and you want to know the probability of rain given that the weather forecast says it's cloudy P(A|B)), you can use conditional probability.

2. It can be thought of as a "revised" probability: Conditional probability gives you the probability of an event occurring within the context of another event. It's as if you're recalculating the probability of event A when you have additional information about event (B).

3. It satisfies the axioms of probability: Conditional probability follows the same axioms as regular probability, which include being non-negative and summing to 1 when considering all possible outcomes.

Conditional probability is a fundamental concept in statistics, machine learning, and many areas of science and engineering. It's widely used for making predictions, making decisions based on data, and understanding the relationships between events.

An example of conditional probabilities  is: 

         i) Not Cloudy and Cloudy in the Morning: 

         Let A be the event "Not Cloudy in the Morning." 

         Let B be the event "Cloudy in the Morning." 

The conditional probability of event B (Cloudy in the Morning) given that event A (Not Cloudy in the Morning) has occurred is denoted as P(B|A). This represents the probability of it being Cloudy in the Morning given that it's Not Cloudy in the Morning. 

         ii) Predict Rain in the Afternoon: 

         Let C be the event "Rain in the Afternoon." 

Then, the conditional probability of event C (Rain in the Afternoon) given that events A and B have occurred is denoted as P(C|A and B). This represents the probability of Rain in the Afternoon given that it's Not Cloudy and Cloudy in the Morning.

Table 3818. Applications of conditional probability.

============================================