=================================================================================

Support-vector machines (SVMs) are a type of supervised learning algorithm used for classification and regression tasks. The primary goal of an SVM is to find a hyperplane that best separates data points belonging to different classes. That is, the goal is to find a hyperplane that maximizes the margin between different classes of data points. This hyperplane is sometimes referred to as the "maximum margin separator" or "optimal margin classifier" because it achieves the maximum separation between classes by having the largest possible margin.  The term "support vector machine" was coined by Vladimir Vapnik and his colleagues in the 1990s:

1. "Support" in "Support Vector Machine":

   • "Support" in SVM refers to the data points used to define the decision boundary between different classes in a classification problem. These data points are called "support vectors."
   • Support vectors are the closest data points to the decision boundary, and they play a crucial role in determining the position and orientation of the boundary. In other words, they support the definition of the decision boundary.
2. "Vector" in "Support Vector Machine":
   • In mathematics and machine learning, a vector is a mathematical object that has both magnitude and direction. In the context of SVM, the term "vector" is used to describe the data points or observations as points in a multidimensional space.
   • Each data point in an SVM is represented as a vector in a feature space, where the dimensions of the space correspond to the features or attributes of the data. SVM works by finding the hyperplane (a higher-dimensional equivalent of a line) that best separates the data points in this feature space.

Figure 4270aa. Support vectors in SVM ( Code).

SVMs are particularly effective in high-dimensional spaces and are well-suited for tasks:

        i) Image classification.

        ii) Text categorization.

In practice, we can simplify SVM as optimization of margin classifier and kernel tricks.

For SVM, we have:

          i) SVMs are often used for binary classification tasks, where the labels are typically represented as -1 and +1 to indicate the two classes, namely, the labels can be given as y ∈ {-1, +1}.

          ii) SVMs aim to separate data into two classes, and the output of an SVM is typically in the form of -1 or +1, indicating the predicted class. That is, it has h output values in {-1, +1}.

          iii) Its decision function is often represented as g(z), where z is the output of the SVM (the result of the dot product between the feature vector and the learned weights), and it is usually expressed as:

                   g(z) = 1 if z ≥ 0

                   g(z) = -1 if z < 0

Text classification, also known as document classification or supervised text categorization, involves assigning predefined labels or categories to text documents based on their content. The goal is to train a model to recognize patterns and associations between the content of documents and the appropriate labels. To do this, you need a labeled dataset where each document is associated with its correct category or label.

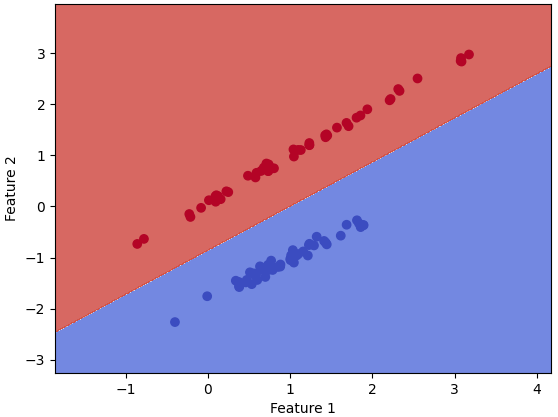
Figure 4270ab. SVM classifier.

As an example of Support Vector Machines (SVM) algorithm applications, assume you want to separate two classes (blue and green) in a way that allows you to correctly assign any future new points to one class or the other. SVM algorithm attempts to find a hyperplane that separates these two classes with the highest possible margin. If classes are entirely linearly separable, then a hard margin can be used. Otherwise, it requires a soft margin, where some points can be treated as outliers. The points that end up on the margins are known as support vectors as shown in Figure 4270b.

Figure 4270b. Illustration of Support Vector Machines (SVM) algorithm.

Key Points:

• Supervised learning: Requires labeled training data.
• Documents are assigned to specific predefined categories.
• Ground truth labels are needed for training and evaluation.
• Common algorithms include Naive Bayes, Support Vector Machines (SVM), and deep learning approaches like Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN).
• Example use case: Categorizing emails as spam or not spam.

Support Vector Machines are a powerful and widely used machine learning algorithm for classification and regression tasks. Support Vector Machine (SVM), [1-2] also called as support-vector networks(SVN), is one of the traditional machine learning models. The function of an SVM is to identify the hyperplane (i.e., decision boundary) with the widest separation between two classes of training data, and thus the SVM is designed to determine the hyperplane at which the margin between two classes of data is maximized.

Support Vector Machines (SVMs) are a class of supervised learning algorithms that can be used for both classification and regression tasks. They are particularly effective in high-dimensional spaces and are widely used for solving complex classification problems.

Basic Concepts:

1. Hyperplane: In a 2-dimensional space, a hyperplane is a line that separates two classes of data points. In higher dimensions, a hyperplane is a flat affine subspace of dimension one less than the ambient space.

2. Margin: The margin is the distance between the hyperplane and the nearest data points from either class. SVM aims to maximize this margin to ensure better generalization to new, unseen data points.

3. Support Vectors: These are the data points that are closest to the hyperplane and directly influence its position and orientation. These points "support" the definition of the hyperplane.

4. Soft Margin and Regularization: In some cases, data might not be perfectly separable by a hyperplane. SVMs can handle this by allowing a certain amount of misclassification (soft margin) and introducing a regularization parameter (C) that controls the trade-off between maximizing the margin and minimizing the classification error.

For SVMs, the decision function is typically given by,

          --------------------------------- [4207a]

where,:

1. h_w,b(x) represents the decision function that classifies a data point x. It returns a value that can be used to determine the class of x.

2. g(z) is often a mathematical function used to determine the class of the data point based on the value of z. In the case of SVMs, it's usually a sign function, which assigns the positive class to one side of the decision boundary and the negative class to the other side. In other words, if g(z) is positive, it assigns one class; if g(z) is negative, it assigns the other class.

3. w is the weight vector that defines the orientation of the decision boundary. It is a parameter learned during the training of the SVM.

4. b is the bias term, also known as the intercept. It is another parameter learned during training, and it shifts the decision boundary away from the origin.

5. x represents the feature vector of the input data point that you want to classify.

6. x ∈ ℝⁿ, b ∈ ℝ.

We can also use the format of logistic regression given by,

          -------------------------------- [4207aa]

with consideration of θ as,

          --------------------------------- [4207ab]

where,

         θ₀ is b in Equation 4207a.

         θ₁, θ₂, and θ₃, represented by w in Equation 4207a.

Working Principle:

Given a labeled training dataset (input data points with corresponding class labels), the goal of SVM is to find the optimal hyperplane that maximizes the margin between the classes. The mathematical formulation involves solving a quadratic optimization problem to determine the hyperplane's parameters.

For a binary classification problem, the objective is to find a hyperplane that satisfies:

          --------------------------------- [4207b]

where:

• w is the weight vector of the hyperplane.
• x_i​ is a data point.
• b is the bias term.
• y_i​ is the class label (y_i = ±1) of the data point x_i where, y_i = +1 for the positive class and y_i = -1 for the negative class.

For SVM, we can transform (θ₀, θ₁, ..., θ_n) into (b, w₁, ..., w_n):

                   ------------------- [4088bb]

Here,θ₀​ to represent the intercept and θ₁, ..., θ_n​ to represent the coefficients of features.

Inequality 4207b is related to the SVM optimization problem, where we try to find a hyperplane defined by the weights (w) and bias (b) that maximizes the margin between two classes. The goal of the SVM is to maximize the margin while ensuring that all data points are correctly classified.

The regularization term is given by,

          --------------------------------- [4207ba]

The regularization term is a form of L2 regularization, which is also known as "ridge regularization" or "Tikhonov regularization." L2 regularization aims to prevent overfitting in machine learning models by adding a penalty term that discourages large values in the weight vector w. In the SVM formulation, you aim to maximize the margin between classes while minimizing the norm of the weight vector (||w||) to prevent overfitting.

By combining Equations 4207a and 4207b, we have,

          --------------------------------- [4207bba]

          ------------------------------ [4207bbb]

          --------------------------------- [4207bbc]

where,

          g is the activation function.

          n is the number of input features.

Equation 4207bba is a basic representation of a single-layer neural network, also known as a perceptron or logistic regression model, depending on the choice of the activation function g. From Equation 4207bba, we can derive different forms or variations by changing the activation function, the number of layers, or the architecture of the neural network as shown in Table 4270a.

Table 4270a. Different forms or variations of Equation 4207bba.

Algorithms	Details
Linear Regression	Set g(z) = z (identity function). This simplifies the equation to , which is the formula for linear regression.
Logistic Regression	Set g(z) = 1 / (1 + e(-z)) (the sigmoid function). This is a binary classification model, and the equation becomes the logistic regression model.
Multi-layer Neural Network	You can add more layers to the network by introducing new sets of weights and biases, and applying activation functions at each layer. This leads to a more complex model.
Different Activation Functions	You can choose different activation functions for different characteristics of your model. For example, you can use ReLU, tanh, or other non-linear activation functions instead of the sigmoid function.
Deep Learning Architectures	You can create more complex neural network architectures, such as convolutional neural networks (CNNs) for image data or recurrent neural networks (RNNs) for sequential data.
Regularization	You can add regularization terms, such as L1 or L2 regularization, to the loss function to prevent overfitting.

The functional margin of hyperplane defined by Equation 4207bb can be given by,

          --------------------------------- [4207bc]

Then, we can have,

          --------------------------------- [4207bd]

where,

          i = 1, 2, ..., m.

Equation 4207bd is used to compute the distance between the data point (x⁽ⁱ⁾, y⁽ⁱ⁾) and the decision boundary by the parameters w and b.

We expect that,

          If y⁽ⁱ⁾ = 1, then we have w^Tx⁽ⁱ⁾ + b >> 0.

          If y⁽ⁱ⁾ = -1, then we have w^Tx⁽ⁱ⁾ + b << 0.

Then, Equation 4207bd will positively be very large in both cases above.

And, as long as Equation 4207bd is greater than 0, then, h(x⁽ⁱ⁾) = y⁽ⁱ⁾. Then, the training set of functional margin is given by,

          --------------------------------- [4207be]

Here, we assume the training is linearly separable.

We have the worst case in (i = 1, 2, ..., n) given by,

          --------------------------------- [4207bf]

We try to make the margin as large as possible.

In SVM, you typically want to find the hyperplane (decision boundary) that maximizes the margin between the classes. The equation for the decision boundary in an SVM is,

          w^Tx⁽ⁱ⁾ + b = 0 --------------------------------------- [4207bg]

In order to ensure that the margin between the classes is determined by the distance of the data points to the hyperplane, rather than the scale of the weight vector, we often normalize the parameters by using,

          --------------------------------- [4207bh]

or,

          --------------------------------- [4207bi]

This normalization doesn't change the orientation of the decision boundary (and thus the classification is not changed) but only scales it to have a unit length. Then, the SVM decision boundary becomes:

          --------------------------------- [4207bj]

This normalization can make the SVM training more numerically stable and helps ensure that all the support vectors lie at a distance of exactly 1 from the decision boundary, simplifying the margin calculation. In practice, many SVM implementations handle this normalization automatically.

The optimization problem aims to minimize the norm of the weight vector (||w||) subject to the constraint that all data points are classified correctly (or with a margin of at least 1).

The classifier of SVMs can be represented by the equation w^Tx + b = 0 . In SVM, this equation defines the decision boundary, which is a hyperplane that separates data points in a binary classification problem. And, one side of the hyperplane represents w^Tx + b > 0 (namely, h_w,b(x) = +1), and the other side represents w^Tx + b < 0 (namely, h_w,b(x) = -1).

For the SVM case, the geometric margin at (x⁽ⁱ⁾, y⁽ⁱ⁾) is given by,

          -------------------------------------- [3815bk]

The signed distance from the decision boundary to the data point (x⁽ⁱ⁾). It indicates which side of the hyperplane the data point falls on. If ŷ⁽ⁱ⁾ is positive, it means the data point is correctly classified, and if it's negative, it's misclassified.

Equation 3815bl below provides a more general expression for ŷ⁽ⁱ⁾, which includes the class label y⁽ⁱ⁾. This is an extension to handle both sides of the decision boundary. If y⁽ⁱ⁾ is positive, the data point should have a positive ŷ⁽ⁱ⁾ to be correctly classified, and if y⁽ⁱ⁾ is negative, ŷ⁽ⁱ⁾ should be negative for correct classification.

          -------------------------------------- [3815bl]

In Support Vector Machines (SVM), the goal of choosing the weight vector "w" and bias term "b" is to maximize the geometric margin for the optimal margin classifier. This choice is fundamental to the SVM algorithm for several reasons:

1. Improved Generalization: Maximizing the geometric margin leads to a classifier that generalizes well to unseen data. A larger margin implies a greater separation between the classes, reducing the risk of overfitting. SVM aims to find a hyperplane that provides the maximum separation between the classes while minimizing classification errors.

2. Robustness: A larger geometric margin results in a more robust classifier. Data points can vary within this margin without affecting the classifier's decision. This robustness is important for handling noise and variations in the data.

3. Margin-Based Classification: SVM is a margin-based classification method. The optimal margin classifier, known as the "maximum margin classifier," is designed to find the decision boundary that maximizes the margin. This decision boundary is precisely what SVM aims to identify.

4. Support Vectors Identification: The maximization of the geometric margin helps in identifying support vectors, which are the data points closest to the decision boundary. These support vectors have a direct impact on the classification and the position of the decision boundary. By maximizing the margin, SVM ensures that only a small subset of the data points (the support vectors) influences the classifier's parameters.

5. Mathematical Foundation: The mathematical formulation of SVM optimization involves finding the weight vector "w" and bias term "b" that maximize the geometric margin while satisfying certain constraints. This mathematical formulation results in a well-defined convex optimization problem, allowing for efficient solutions.

6. Simplified Decision Boundary: A larger geometric margin often results in a simpler decision boundary. This simplicity makes the classifier more interpretable and efficient during classification.

7. Controlled Trade-off: By maximizing the geometric margin, SVM implicitly controls the trade-off between minimizing classification errors (maximizing the functional margin) and maximizing the margin. This leads to a balanced classification model.

Equation 3815bm shows to how to maximize the geometric margin (γ) for the optimal margin classifier:

          -------------------------------------- [3815bm]

This inequality is hard to address if we do not use a gradient descent and initially known local optima, then it implies that y⁽ⁱ⁾(w^Tx⁽ⁱ⁾ + b) ≥ 0, because:

Multiply both sides of Inequality 3815bm by ||w||:

          --------------------------- [3815bn]

Let ϒ ' =ϒ ||w||, so the inequality becomes:

          --------------------------- [3815bo]

Now, because ||w|| is a positive value and γ is also non-negative (γ ≥ 0), γ' is still non-negative (γ' ≥ 0). Thus, y⁽ⁱ⁾(w^Tx⁽ⁱ⁾ + b) ≥ 0 holds.

Based on Inequality 3815bm, we can have,

          --------------------------- [3815bp]

Multiply both sides by ||w||, then we have,

          --------------------------- [3815bq]

Now, the key insight is that the margin between the two classes, which is 2/||w||, is maximized when 1/||w|| is maximized. Thus, 1/||w|| is the quantity we want to maximize, and we can rewrite it as:

          --------------------------- [3815br]

Therefore, to maximize 1/||w||, we need to minimize the denominator to be 1. This constraint ensures that data points are correctly classified, and the margin is maximized.

For the margin, we have,

          --------------------------- [3815bra]

The decision boundary of an SVM is defined by the hyperplane w^Tx + b = 0. The vector w is orthogonal (perpendicular) to this decision boundary. As an example, if w is , then the first component of the vector (2 in this case) represents the x-coordinate, and the second component (1 in this case) represents the y-coordinate of the point in 2D plane. Figure 4270ba shows the optimization of w and b to satisfy the formulas 4207b and 4207ba in order to find a hyperplane.

Figure 4270ba. Optimization of w and b to satisfy the formulas 4207b and 4207ba. Code.

Figure 4270bb shows the calculation of the distances of the points to the hyperplane with Inequality 3815bm.

Figure 4270bb. Calculation of the distances of the points to the hyperplane. Code.

In SVMs, for training examples x(i), we can assume,

          --------------------------- [3815bs]

SVMs work by finding a hyperplane that best separates data points in a high-dimensional and even infinite-dimensional space. The Representer Theorem is a theoretical result in kernel machines. If the data can be mapped into a high-dimensional feature space using a kernel function, then the solution to the optimization problem in the SVM formulation can be expressed as a linear combination of the training examples in that feature space.

With more complicated expression, Equation 3815bs can be given by,

          --------------------------- [3815bs]

Where:

• α_i​ are the Lagrange multipliers or dual variables (non-negative for support vectors) associated with the training data points.
• y⁽ⁱ⁾ is the target output (or called class labels) for the i-th training data point, which is equal to +1 and -1.
• x⁽ⁱ⁾ is the i-th training data point, namely the feature vectors of the data points.

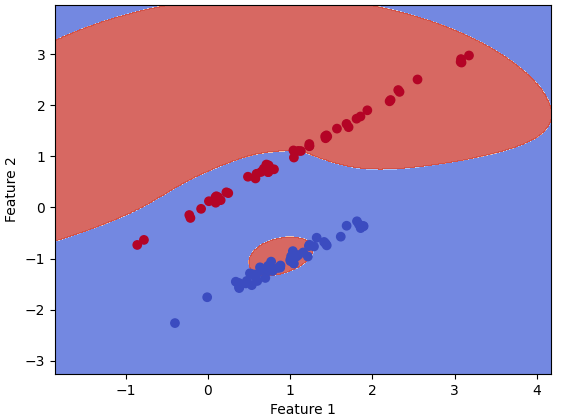
Plug Equation 3815bs into Equation [4207ba, we can have,

          --------------------------- [3815bt]

Using the properties of the norm and the dot product,

          --------------------------- [3815bu]

Then, we can expand the dot product,

          --------------------------- [3815bv]

It can be written as,

          --------------------------- [3815bw]

where,

          <x⁽ⁱ⁾, x^(j)> represents the inner product (or dot product) between the data points x⁽ⁱ⁾ and x^(j), e.g. two different vectors, where is the only place in which the feature vectors appear.

          is a double summation. Here, i and j are typically two indices representing different data points. y⁽ⁱ⁾ and y^(j) are labels associated with these data points.

To find the minimum of (1/2)||w||², we need to minimize it with respect to w, subject to the constraints imposed by the Lagrange multipliers and the data points.

The optimization problem can be stated as:

Minimize (1/2)||w||² with respect to w, subject to the constraints:

          --------------------------- [3815ca]

This is a quadratic optimization problem with linear constraints. We can use techniques like the Lagrange multiplier method or a quadratic programming solver to find the minimum of (1/2)||w||² subject to these constraints. The solution will give you the optimal values of α_i​ , and from that, you can compute the minimum value of (1/2)||w||². The solution will also give us the optimal values of w, which will be the decision boundary for a support vector machine (SVM) classifier.

Then, the question is to maximize the term below:

          ----------------------- [3815cb]

Subject to:

          ----------------------------------------------------- [3815cc]

          ----------------------- [3815cd]

The one, presented by the formulas 3815cb, 3815cc and 3815cd, is the dual form of the SVM optimization problem. The dual form is often used due to its computational benefits and strong duality properties. The objective of this optimization problem is to find the optimal values of α_i​ that maximize the margin while satisfying the constraints. The two statements 3815cc and 3815cd are common conditions in the context of support vector machines (SVMs), and they are often associated with the Karush-Kuhn-Tucker (KKT) conditions for SVM optimization problems. In SVM, the Lagrange multipliers (α_i) should be greater than zero. These non-zero values of α_i​ correspond to support vectors, which are the data points that are closest to the decision boundary (the support vectors define the position of the decision boundary). These support vectors have non-zero Lagrange multipliers. The constraint 3815cd ensures that the Lagrange multipliers are chosen in a way that satisfies the SVM duality conditions. Specifically, it enforces the complementary slackness condition, which implies that either α_i i​ is zero or the corresponding data point is correctly classified and lies on or within the margin. In other words, this condition ensures that for correctly classified points (those on or within the margin), α_i​ will be non-zero, and for incorrectly classified points (those outside the margin), α_i​ will be zero.

In dual problem for the SVM, Inequality 3815cd is modified as following,

          ----------------------- [3815ccb]

where,

          C is the regularization parameter that controls the trade-off between maximizing the margin between the classes and minimizing the classification error.

SVMs can be extended to handle non-linearly separable data by using the "kernel trick." The kernel function computes the inner product of data points in a higher-dimensional space without explicitly transforming the data. This allows SVMs to effectively capture complex relationships between features.

The steps of how kernels are applied in machine learning, particularly in the SVMs and kernel methods are:

          1) Write algorithm in terms of <x⁽ⁱ⁾, x^(j)> (or <x, z>): This step involves expressing the algorithm or model in terms of the dot product between input data points. This is typically done when you have a linear algorithm, and you want to extend it to work in a higher-dimensional feature space without explicitly computing the transformation.

          2) Let it map from your input feature x to some high-dimensional set of feature φ(x): In this step, you can map your original data from a lower-dimensional feature space to a higher-dimensional feature space using a function φ(x). This mapping can be complex and computationally expensive, but it's a key concept in kernel methods.

          3) Find a way to compute:

          ------------------ [3815ce]

          where,

          This is where the kernel trick comes into play. Instead of explicitly computing the high-dimensional feature vectors φ(x) and φ(z), you find a kernel function K(x, z) that allows you to compute the dot product in the higher-dimensional space without explicitly mapping the data points. Common kernel functions include the linear kernel, polynomial kernel, and radial basis function (RBF) kernel.

          4) Replace <x, z> in the algorithm with K(x, z): This is the final step where you substitute the original dot product <x, z> in your algorithm with the kernel function K(x, z). This allows you to work in the high-dimensional feature space without the computational cost of explicitly computing φ(x) and φ(z).

Support Vector Machines are a powerful and flexible tool in the realm of machine learning, often used for various real-world applications like image classification, text classification, and bioinformatics.

There are several Python libraries that you can use to train Support Vector Machine (SVM) models. Some of the popular ones include:

1. scikit-learn: Scikit-learn is one of the most widely used machine learning libraries in Python. It provides a simple and consistent interface for various machine learning algorithms, including SVM. The SVC class in scikit-learn is used to train Support Vector Machine models.

2. LibSVM: LibSVM is a widely used library specifically designed for Support Vector Machines. While it has its own C/C++ implementation, there is also a Python wrapper called svmutil that allows you to use LibSVM from Python.

3. SVMLight: Similar to LibSVM, SVMLight is another popular library for SVM. It has a Python wrapper called svmlight-loader.

4. XGBoost: XGBoost is primarily known for gradient boosting, but it also has an implementation of SVM called xgboost.XGBClassifier which can be used for SVM-based classification.

5. C-Support Vector Classification (CVXOPT): CVXOPT is a Python library for convex optimization. It provides an implementation of SVM for classification tasks.

6. TensorFlow: TensorFlow, a popular deep learning library, includes an implementation of SVM as part of its toolkit. You can use the tf.compat.v1.estimator.SVC class to train SVM models.

7. PyTorch: Similarly, PyTorch, another deep learning library, offers an implementation of SVM through its torchsvm module.

8. Shogun: Shogun is a machine learning toolbox that provides SVM implementations along with other algorithms. It is designed for large-scale learning tasks.

For most general use cases, scikit-learn is the recommended choice due to its user-friendly interface, extensive documentation, and active community support. However, you might choose a different library based on specific requirements or if you are working on a particular research project.

SVMs are a set of supervised learning methods used for:
         i) Classification,
         ii) Regression,
         iii) outliers detection.

The advantages of SVMs are:
         i) Effective in high dimensional spaces.
         ii) Still effective in cases where number of dimensions is greater than the number of samples.
         iii) Can handle non-linearly separable data using kernel functions.
         iv) Maximum margin concept leads to good generalization.
         v) Less prone to overfitting (with proper tuning of hyperparameters).
         vi) Versatile - can be used for both classification and regression.
         vii) Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.
         viii) Versatile: different Kernel functions can be specified for the decision function. Common kernels are provided, but it is also possible to specify custom kernels.

The disadvantages and limitations of SVMs are:
         i) If the number of features is much greater than the number of samples, avoid over-fitting in choosing Kernel functions and regularization term is crucial.
         ii) SVMs do not directly provide probability estimates, these are calculated using an expensive five-fold cross-validation.
         iii) Can be computationally expensive for large datasets.
         iv) Choice of kernel and hyperparameters can impact performance.
         v) Interpretability of results can be challenging.
         vi) SVM might struggle with noisy datasets.

The reasons why SVMs is less prone to overfitting are mainly due to the structural risk minimization principle and the margin maximization concept:

1. Margin Maximization: SVMs aim to find a hyperplane that maximizes the margin between the two classes of data points. The margin is the distance between the hyperplane and the nearest data points (support vectors). By maximizing the margin, SVMs seek a decision boundary that separates the classes with a wide gap, making them more robust to noise and less likely to overfit.

2. Structural Risk Minimization: SVMs are designed to minimize the structural risk, which is a combination of empirical risk (training error) and the complexity of the model. This means that SVMs strive to find a balance between fitting the training data and keeping the model as simple as possible. The use of a regularization term that penalizes (minimizes) the magnitude of the weight vector (||w||²) contributes to this goal. Regularization discourages the model from fitting the training data too closely, which can help prevent overfitting.

3. Kernel Trick: While it's true that SVMs can use kernel functions to implicitly map data into higher-dimensional spaces, this technique helps SVMs capture more complex, non-linear decision boundaries when needed. However, the focus remains on maximizing the margin and minimizing overfitting, not solely on achieving infinite dimensions. Kernels help represent non-linear relationships efficiently without explicitly working in infinite-dimensional spaces.

Figure 4270bc shows the flowchart of WMFPR (wafer map failure pattern recognition) which is based on a two-stage framework. Stage 1 determines whether a wafer map exhibits a failure pattern, while Stage 2 identifies the pattern type. In this flowchart, an SVM is used as a classifier. During the training phase, the SVMs determine the support vectors in the training data, which are applied to predict new wafer maps during the test phase. The main advantage of the two-stage framework is that the parameters can be trimed to optimize the tradeoff between the false-positive rate and the false-negative rate at Stage 1.

In ML programming, we need to include the minimization of objective function:

                      -------------------------------------- [3815dy]

where,

• ||w||²: This term represents the squared Euclidean norm of the weight vector � w. Minimizing this term encourages finding a solution with a small weight vector, promoting simplicity.

• CΣξ_i: This term represents the regularization parameter C multiplied by the sum of the slack variables ξ_i. The regularization parameter C controls the trade-off between having a smooth decision boundary and classifying the training points correctly. The sum of slack variables penalizes misclassifications and encourages a more robust model.

The objective of the SVM is to minimize the combination of these two terms.

The program also need to include the subject to constraint:

                      ------------------------ [3815ey]

This constraint ensures that each training example is correctly classified, with a margin of at least 1. The slack variable ξ_i​ allows for some flexibility, allowing points to be on the wrong side of the decision boundary but penalizing such misclassifications in the objective function.

Machine learning methods such as logistic regression, SVM with a linear kernel, and so on, will often require that categorical variables be converted into dummy variables. For example, a single feature Vehicle would be converted into three features, Cars, Trucks, and Pickups, one for each category in the categorical feature. The common ways to preprocess categorical features are:
        i) pandas,
        ii) scikit-learn.

Support Vector Machines (SVM) are a versatile and powerful machine learning algorithm used for both classification and regression tasks. Here are some applications of Support Vector Machines:

1. Image Classification: SVMs have been widely used for image classification tasks, such as object recognition, facial expression recognition, and medical image analysis.

2. Text Classification and Sentiment Analysis: SVMs can be used to classify text data into different categories, such as spam detection, sentiment analysis, and topic categorization.

3. Prediction models: classifying news articles into predefined categories, separating spam emails from non-spam, etc.
4. Bioinformatics: SVMs are employed in tasks like protein structure prediction, gene expression classification, and disease classification based on biomarkers.
5. Handwriting Recognition: SVMs can be used for character recognition and handwriting analysis, such as recognizing handwritten digits in postal codes.
6. Anomaly Detection: SVMs are useful for detecting outliers or anomalies in data, which can be valuable in fraud detection, network security, and industrial equipment monitoring.
7. Speech Recognition: SVMs have been utilized in speech recognition systems to classify phonemes and recognize spoken words.
8. Financial Forecasting: SVMs can be applied to predict stock prices, market trends, and other financial indicators.
9. Face Detection: SVMs are often used in face detection applications to determine whether an image contains a face or not.
10. Medical Diagnostics: SVMs can assist in medical diagnosis tasks, such as identifying diseases based on patient data or medical images.
11. Remote Sensing: SVMs are employed in remote sensing applications for land cover classification, environmental monitoring, and satellite image analysis.
12. Quality Control: SVMs can be used for quality control in manufacturing processes to classify defective and non-defective products.
13. Geological Surveying: SVMs can help classify geological features based on data collected from sensors or satellite images.
14. Recommendation Systems: SVMs can be used in recommendation systems to classify and recommend items to users based on their preferences and behavior.
15. Protein Structure Prediction: SVMs are used in predicting the structure of proteins based on their amino acid sequences.
16. Marketing and Customer Segmentation: SVMs can help segment customers based on their behaviors, preferences, and demographics for targeted marketing campaigns.
17. Natural Language Processing (NLP): SVMs are utilized in NLP tasks like named entity recognition, text categorization, and text summarization.

These are just a few examples, but SVMs can be applied to a wide range of domains and problems where classification or regression is required.

Table 4270bb lists SVMs with different Kernel visulizations.

Table 4270bb. SVMs with different Kernel visulizations.

Kernel	Formula	Visulization
Linear Kernel		code
Polynomial Kernel		code code
Radial Basis Function (RBF) Kernel (Gaussian Kernel)		code
Sigmoid Kernel		code
Laplacian Kernel		code
Bessel Function Kernel		code

As shown in Table 4270c, batch gradient descent can also be used for training SVMs, particularly for solving the soft-margin SVM optimization problem. However, note that SVMs are often trained using optimization algorithms that are specifically designed for their objective function, such as the Sequential Minimal Optimization (SMO) algorithm and the gradient descent-like Pegasos algorithm. These specialized methods can be more efficient than using standard batch gradient descent for SVM training. Here, we assume w is a linear combination of the training examples.

Figure 4270bd shows comparison between hard margin without C and soft margin with C in SVMs see page3808.

Table 4270c. Algorithms used by SVM.

============================================

Defect Detection and Classification. Code:
         
       Output:    
         
         

============================================

[1] Ming-Ju Wu, Jyh-Shing R. Jang, and Jui-Long Chen, Wafer Map Failure Pattern Recognition and Similarity Ranking for Large-Scale Data Sets, IEEE TRANSACTIONS ON SEMICONDUCTOR MANUFACTURING, 28(1), Feb 2015.
[2] C. Cortes and V. Vapnik, “Support vector networks,” Mach. Learn., vol. 20, no. 3, pp. 273–297, Sep. 1995.