| It was proposed by August and Wernisch [1] that backscattering coefficient (η) of electrons can be given by,
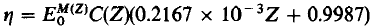 ------------- [4564a] ------------- [4564a]
where
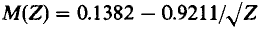
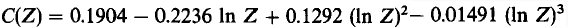
This analytical expression was derived with good fit to experimental data, especially with regard to low electron energies. Figure 4564a shows the comparison of backscattering coefficient between experimentally fitted Equation and Monte Carlo (MC) simulation for C, Si, and Cu. Good agreement is
obtained to within 10% of the analytical expression. η can be further classified to coefficients of elastic backscattering electrons and coefficients of inelastic backscattering electrons.
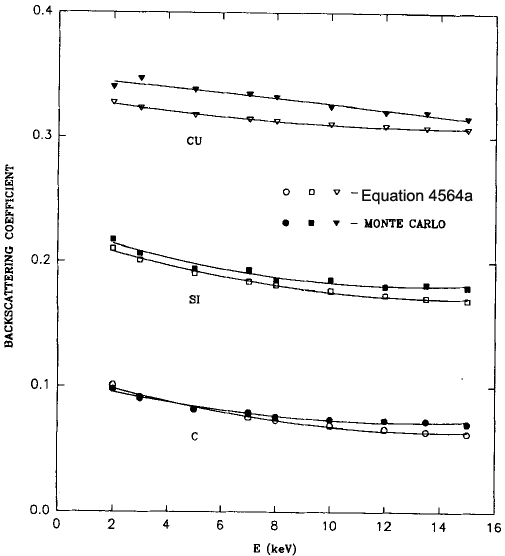
Figure 4564a. Comparison of backscattering coefficient between experimentally fitted Equation
and Monte Carlo (MC) simulation for C, Si, and Cu [2].
When the angle of incidence of the electron beam to a sample is increased, the backscattered electron yield increases.
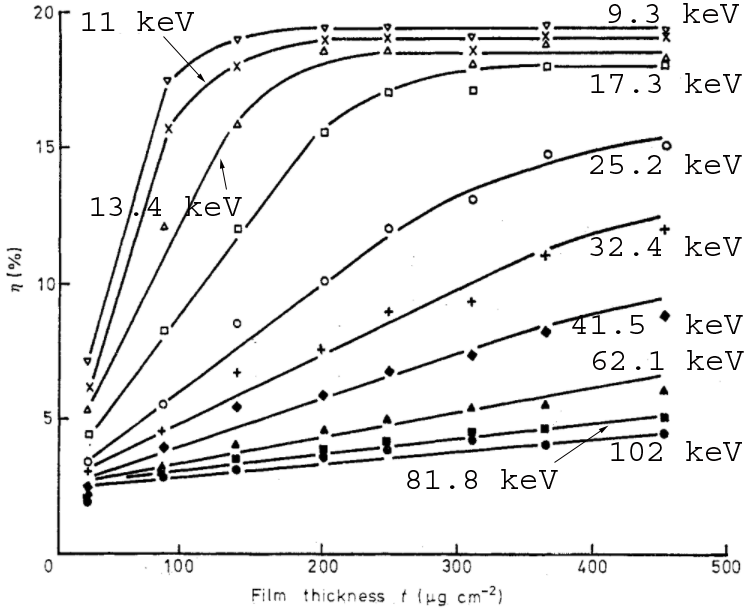
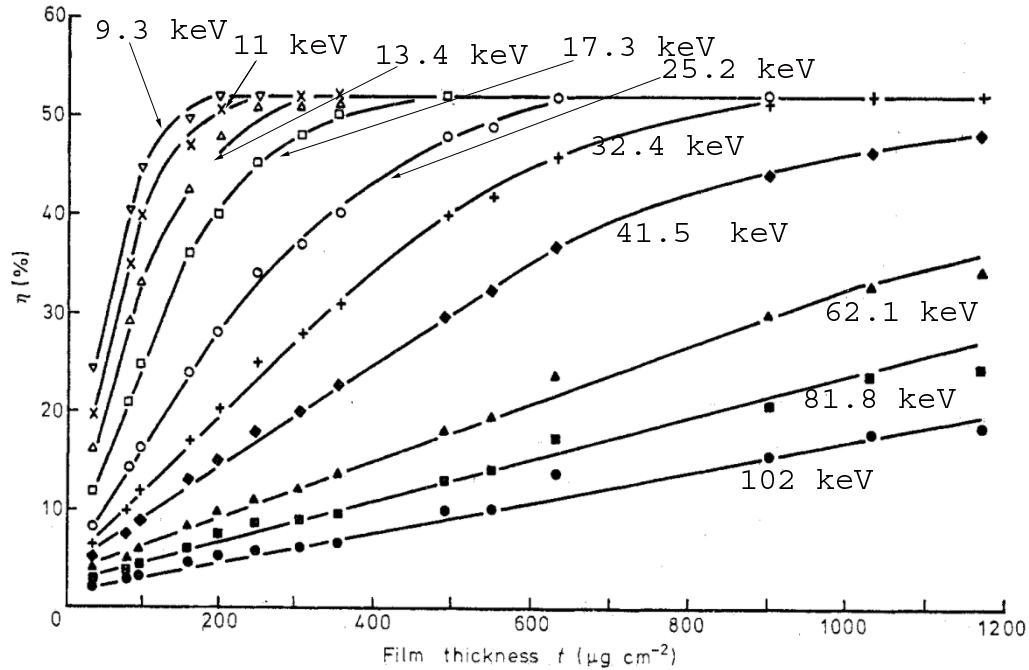
Figure 4564b shows the backscattering coefficient, η, on the electron incident surface as a function
of the thickness, t, for Al and Au films at different energies of the incident
electrons.
 |
 |
(a) |
(b) |
| Figure 4564b. Backscattering coefficient, η, on the electron incident surface as a function
of the thicknesses, t, at different energies of the incident
electrons: (a) Al, and (b) Au films. Adapted from [3] |
| Table 4564. Calculated backscattering electron yields versus the primary electron energy for electron normally incident on targets. |
| Element |
100 eV |
125 eV |
150 eV |
175 eV |
200 eV |
250 eV |
300 eV |
350 eV |
400 eV |
500 eV |
600 eV |
800 eV |
1 keV |
1.25 keV |
1.5 keV |
2.0 keV |
2.5 keV |
3.0 keV |
4.0 keV |
5.0 keV |
6.0 keV |
8.0 keV |
10 keV |
12.5 keV |
15.0 keV |
20.0 keV |
25.0 keV |
29.7 keV |
| Al |
0.1639 |
0.1891 |
0.2055 |
0.2175 |
0.2252 |
0.2345 |
0.2392 |
0.2398 |
0.2379 |
0.2338 |
0.2293 |
0.2190 |
0.2104 |
0.2020 |
0.1951 |
0.1852 |
0.1786 |
0.1734 |
0.1664 |
0.1621 |
0.1590 |
0.1548 |
0.1523 |
0.1492 |
0.1473 |
0.1436 |
0.1421 |
0.1414 |
| Si |
0.1647 |
0.1888 |
0.2053 |
0.2172 |
0.2242 |
0.2343 |
0.2400 |
0.2425 |
0.2435 |
0.2419 |
0.2371 |
0.2298 |
0.2208 |
0.2131 |
0.2062 |
0.1965 |
0.1897 |
0.1840 |
0.1779 |
0.1745 |
0.1704 |
0.1665 |
0.1641 |
0.1623 |
0.1608 |
0.1594 |
0.1572 |
0.1568 |
| Ni |
0.2033 |
0.2447 |
0.2745 |
0.2973 |
0.3130 |
0.3327 |
0.3424 |
0.3482 |
0.3506 |
0.3510 |
0.3486 |
0.3416 |
0.3349 |
0.3284 |
0.3226 |
0.3172 |
0.3136 |
0.3119 |
0.3109 |
0.3106 |
0.3100 |
0.3071 |
0.3070 |
0.3056 |
0.3046 |
0.3046 |
0.3043 |
0.3044 |
| Cu |
0.1789 |
0.2270 |
0.2632 |
0.2904 |
0.3114 |
0.3369 |
0.3519 |
0.3607 |
0.3654 |
0.3667 |
0.3648 |
0.3571 |
0.3482 |
0.3401 |
0.3330 |
0.3244 |
0.3194 |
0.3169 |
0.3143 |
0.3122 |
0.3108 |
0.3082 |
0.3073 |
0.3052 |
0.3035 |
0.3001 |
0.2969 |
0.2956 |
| Mo |
0.1428 |
0.1692 |
0.2020 |
0.2337 |
0.2601 |
0.2988 |
0.3237 |
0.3386 |
0.3491 |
0.3620 |
0.3699 |
0.3785 |
0.3844 |
0.3887 |
0.3912 |
0.3932 |
0.3955 |
0.3944 |
0.3928 |
0.3933 |
0.3939 |
0.3934 |
0.3950 |
0.3980 |
0.4017 |
0.4052 |
0.4102 |
0.4117 |
| Rh |
0.1649 |
0.1777 |
0.2010 |
0.2279 |
0.2529 |
0.2936 |
0.3195 |
0.3369 |
0.3489 |
0.3621 |
0.3710 |
0.3792 |
0.3841 |
0.3902 |
0.3925 |
0.3971 |
0.3996 |
0.3996 |
0.3988 |
0.3980 |
0.3986 |
0.3981 |
0.3994 |
0.4020 |
0.4035 |
0.4081 |
0.4127 |
0.4169 |
| Os |
0.1039 |
0.0849 |
0.0809 |
0.0866 |
0.1018 |
0.1427 |
0.1947 |
0.2451 |
0.2890 |
0.3565 |
0.3996 |
0.4421 |
0.4606 |
0.4709 |
0.4747 |
0.4775 |
0.4775 |
0.4785 |
0.4795 |
0.4813 |
0.4818 |
0.4873 |
0.4916 |
0.4981 |
0.5032 |
0.5125 |
0.5208 |
0.5264 |
| Ir |
0.1081 |
0.0865 |
0.0788 |
0.0802 |
0.0902 |
0.1239 |
0.1672 |
0.2121 |
0.2526 |
0.3168 |
0.3590 |
0.4053 |
0.4250 |
0.4376 |
0.4434 |
0.4478 |
0.4506 |
0.4514 |
0.4546 |
0.4575 |
0.4611 |
0.4655 |
0.4709 |
0.4770 |
0.4831 |
0.4932 |
0.5028 |
0.5081 |
| Pt |
0.1044 |
0.0828 |
0.0735 |
0.0743 |
0.0828 |
0.1162 |
0.1612 |
0.2104 |
0.2549 |
0.3238 |
0.3678 |
0.4152 |
0.4348 |
0.4483 |
0.4528 |
0.4571 |
0.4589 |
0.4598 |
0.4620 |
0.4655 |
0.4673 |
0.4735 |
0.4777 |
0.4835 |
0.4890 |
0.4986 |
0.5078 |
0.5142 |
| Au |
0.1073 |
0.0860 |
0.0757 |
0.0740 |
0.0807 |
0.1078 |
0.1487 |
0.1937 |
0.2357 |
0.3040 |
0.3486 |
0.3979 |
0.4217 |
0.4351 |
0.4426 |
0.4489 |
0.4516 |
0.4539 |
0.4567 |
0.4588 |
0.4622 |
0.4687 |
0.4740 |
0.4788 |
0.4833 |
0.4904 |
0.4964 |
0.4997 |
[1] H. J. August and J. Wernisch, Phys. Status Solidi 114, 629 (1 989).
[2] C. L. Lee and C. K. Ong, Bethe Ionization Cross-sections: a Quantitative Survey on Calculating the Backscattering Factor in AES, Surface and Interface Analysis, 19, 227-231 (1992).
[3] L Reimer and H Drescher, Secondary electron emission of 10-100 keV electrons from transparent fdms of A1 and Au, J. Phys. D: Appl. Phys., Vol. 10, 1977.
|
