Practical Electron Microscopy and Database

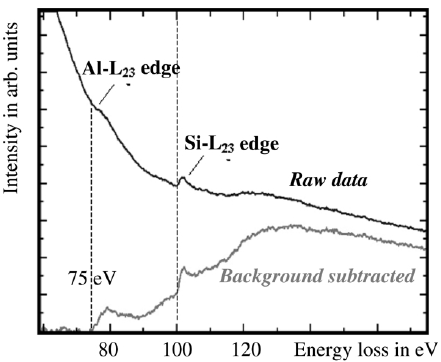
These characteristic ionization edges in EELS are superimposed on a background intensity due to zero-loss and plasmon peaks and the tails of edges lying at lower energies. The separation of energy loss signal from the background is necessary for extracting elemental information for elemental quantification and mapping. Due to the complexity of process contributing to the background, it is not possible to model the background from first principles. The method usually performed to calculate the background is to estimate the background contribution under the edge from the pre-edge area. The background can first be estimated and subsequently extrapolated to higher energies to subtract it from the core-loss region.

Because of the similarities in signal extraction between EELS and EFTEM the same statistical extrapolation can be applied. Different methods for background subtraction have been proposed by numerous researchers [1 - 4]. Depending on the complexity of the chosen model, different number of filtered images at different energy losses in front of the core-edge has to be recorded according to the number of fitting parameters for the background subtraction.

The EEL spectra in Figure 4723a show the Al L_2,3 edge as well as the Si L_2,3 edge after background subtraction, taken from Al_xSi_yO_z matrix. Note that the background subtraction was done by referring to the first edge in the profile (Al L_2,3 edge here).

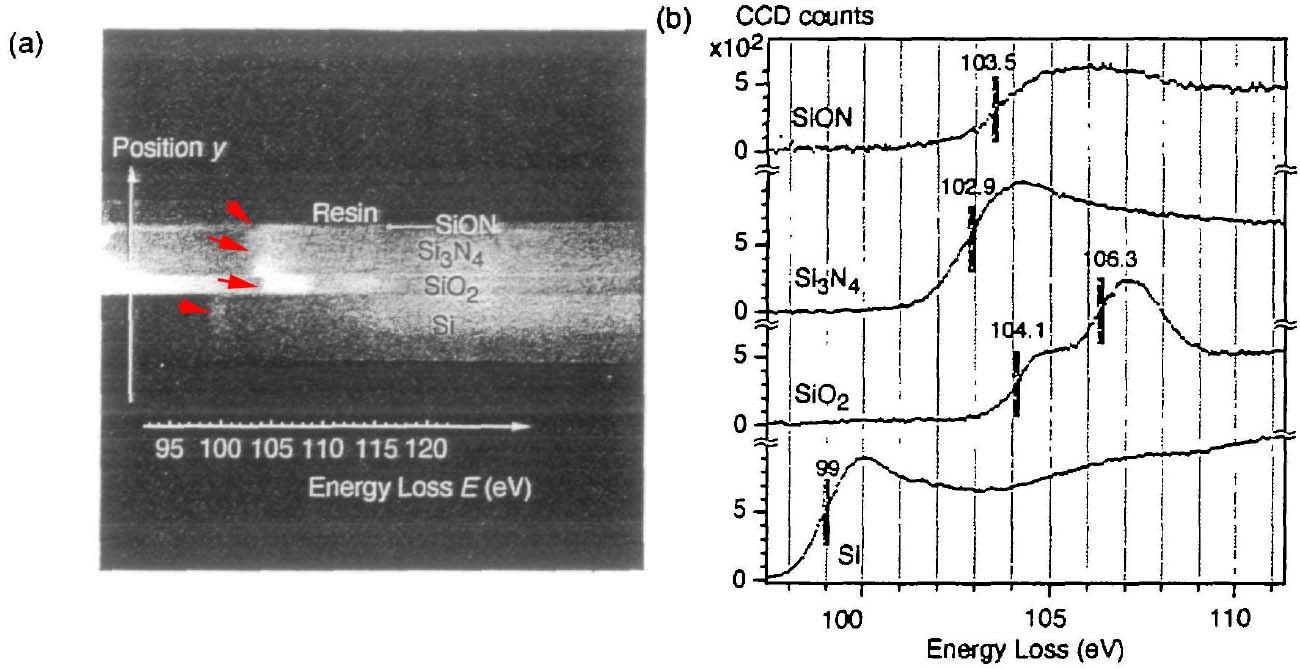
Figure 4723b shows that the chemical shifts are revealed by spatially resolved EELS of Si-L_2,3 edges. Figure 4723b (a) shows the 2-D (two-dimensional) spectrum image obtained by an energy filter. Note that this image shows the image contrast before background subtraction. The vertical axis corresponds to the location (y) in the layered materials of SiON. Si₃N₄, SiO₂ and pure Si. The horizontal axis corresponds to the energy loss E. Energy dispersion used here was 0.051 eV per pixel. The energy range ΔE recorded in the 2-D spectrum image was 52 eV (= 88 - 141 eV in energy loss). Both the shift of the bright lines (shown by red arrows) in Figure 4723b (a) and the vertical lines in Figure 4723b (b) indicate the chemical shift of Si-L_2,3 edges. Figure 4723b (b) shows energy loss spectra of each layer extracted from Figure 4723b (a). Here, the backgrounds of the spectra were subtracted.

Figure 4723b. The spatially resolved EELS analysis of Si-L_2,3 edges, (a) 2-D spectrum
image and (b) spectra of SiON. Si₃N₄, SiO₂ and pure Si. Adapted from [4]

In EELS quantitative analysis, this background contribution I_b must be subtracted to obtain the core-loss signal I_k,
         I_k = I_t - I_b ------------------------------------------- [4723a]
where,         
          I_t -- the total integrated intensity over the core-loss integration range.

The background (due mainly to the contribution of valence electrons) removal in EELS is much more different than in EDS because of the complexity and heterogeneity of the shape of the various edges. A couple of techniques have been proposed to subtract the background effects in EELS analysis and EFTEM mapping:
         i) Such problems of the background removal in EELS can be partially overcome by having standard materials to obtain information of approximate edge shapes and intensities, and using such calculated information to the experimental spectrum for the background correction.
         ii) The background can be modelled and removed with the use of the inverse power-law model (AE^-r) as shown in the examples in Table 4723.

Table 4723. Examples of background removal with inverse power-law model.

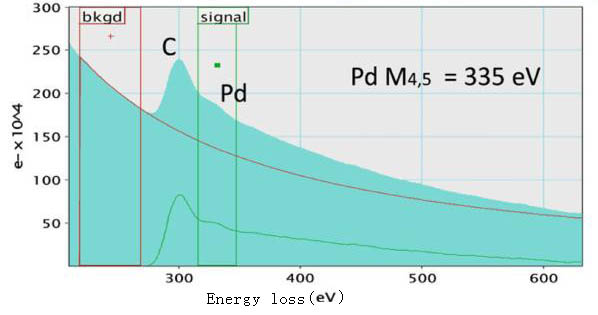
Figure 4723c shows an EEL spectrum, presenting Pd-M_4,5 edge at 335 eV, taken from a Pd nanoparticle on holey carbon (C) film. Both the C and Pd signals are clear. In order to extract the Pd signal, the energy window for background subtraction is selected before the C K edge but not immediately before the Pd-M₄ edge onset since there is uncertainty which is induced by the carbon peak.

In many cases, the background window cannot be too big since the energy peaks of other possible elements in the specimen are very close to the core-loss of the interesting element. For instance, for a core loss of the interesting element is about 348 eV, a small background window (e.g. 20 eV) is used to fit the spectrum in order to avoid the contribution from the carbon edge (284 eV), so that we only pick up the signal generated by the interesting element for the elemental evaluation.

         iii) The simplest approach of subtracting the background intensity in EFTEM elemental maps is ratio mapping, where the post-edge intensity I_post is divided by the pre-edge intensity I_pre. If the shape of the background remains constant across the entire image, then the ratio value k gives a simple representation of the distribution of an element by,
                  k = I_post/I_pre ---------------------------------------- [4723b]
However, it is more useful to obtain a modified ratio k_sub by subtracting k₀, which corresponds to the measured ratio value in a region of the specimen where the element is known to be absent,
                  k_sub = I_post/I_pre - k₀ ---------------------------------------- [4723c]
Multiplication of this equation by the pre-edge intensity gives the so-called ‘two-window’ intensity,
                  S(Δ,β) = I_post - k₀I_pre ---------------------------------------- [4723d]
where,
          Δ -- the energy width of the integration window above the core edge,
          β -- the collection semi-angle of the scattered electrons accepted by the imaging filter, as defined by the objective aperture.
However, when the specimen thickness or composition varies significantly over the field of interest, such two-window technique can become invalid.
In this case, three-window method, in which two images are collected below the core-edge for fitting the pre-edge background intensity as an inverse power function, has been very useful for mapping the distributions of elements, provided that the background under a core-edge of interest follows an inverse power law. However, the fitting of two parameters in the three-window method, rather than one parameter in the two-window method, has the undesirable effect of increasing the statistical noise in the background estimation. [7]

[1] Bentley, J., Lehmann, G. L., Sklad, P. S., 1982. Alternative background fitting for electron energy-loss spectra. In Proc. 40th Annual EMSA
Meeting, ed G. W. Bailey, pp. 496 497. Claitor’s, Baton Rouge.
[2] Bonnet, N., Colliex, C., Mory, C., Tence, M., 1988. Developments in processing image sequences for elemental mapping. Scanning
Microscopy, Supplement, Vol. 2, pp. 351 364. Scanning Microscopy International, Chicago, IL.
[3] Tenailleau H., Martin J. M., 1992. A new background subtraction for lowenergy EELS core edges. J. Microsc., 166, 297–306.
[4] Koji Kimoto, Tomoko Sekiguchi and Takashi Aoyama, Chemical shift mapping of Si L and K edges using spatially resolved EELS and energy-filtering TEM, Journal of Electron Microscopy 46(5): 369-374 (1997).
[5] I. Sieber, R. Schneider, I. Doerfel, P. Schubert-Bischoff, S. Gall, W. Fuhs, Preparation of thin polycrystalline silicon films on glass by aluminium induced crystallisation—an electron microscopy study, Thin Solid Films 427 (2003) 298–302.
[6] R. Esparza, Amado F. García-Ruiz, J. J. Velázquez Salazar, R. Pérez, and M. José-Yacamán, Structural characterization of Pt–Pd core–shell nanoparticles by Cs-corrected STEM, J Nanopart Res. 2012 Dec; 15(1342).
[7] M. A. Aronova, Y. C. Kim, G. Zhang, and R. D. Leapman, Quantification and Thickness Correction of EFTEM Phosphorus Maps, Ultramicroscopy, 107(2-3): 232–244, 2007.