|
||||||||
State Transition Function (Probability) in Reinforcement Learning - Python Automation and Machine Learning for ICs - - An Online Book - |
||||||||
| Python Automation and Machine Learning for ICs http://www.globalsino.com/ICs/ | ||||||||
| Chapter/Index: Introduction | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Appendix | ||||||||
================================================================================= In a reinforcement learning problem, if we are dealing with an environment where the outcomes of actions are uncertain or not precisely known, then the transition probabilities cannot be known. In such cases, we may need to employ model-free reinforcement learning approaches, where we don't explicitly model the transition probabilities and instead learn them through interaction with the environment. An empirical estimate of the transition probability, Ps,a, can be given by, where,
Equation 3676a is a maximum likelihood estimate (MLE) of the transition probability in the sense that it is derived from observed frequencies of events in the data. The idea is that, in a model-free setting, you can estimate the transition probabilities based on the frequency of observed transitions during the agent's interactions with the environment. The more times the agent takes action in state and observes the resulting transition to state s', the higher the estimate of the transition probability. This ratio in Equation 3676a is a form of empirical estimation based on the observed data. Note that this kind of estimation is applicable when the agent is learning from experience and does not have explicit knowledge of the transition probabilities. The estimation becomes more accurate as the agent gathers more data through interactions with the environment. However, in Equation 3676a can lead to a situation where the ratio is 0/0 if (i.e., no instances of action in state ) and (i.e., no instances of the transition from to when taking action ). In such cases, a common practice is to use a default or smoothing value to avoid division by zero. The choice of the default value depends on the context and the characteristics of the problem. In many cases, 1/|S| is used as a default value, where |S| is the total number of states in the environment. This approach is a form of Laplace smoothing or add-one smoothing, where a small constant is added to all observed counts to ensure that no probability estimate is exactly zero. Then, we can modify Equation 3676a to, This modification helps prevent division by zero and provides a more robust estimate, especially in cases where the agent has limited data and encounters unseen state-action pairs. Two common model-free reinforcement learning methods are Q-learning and Monte Carlo methods:
In both cases above, these model-free methods are advantageous when we don't have access to the dynamics of the environment. They rely on the observed data (state-action pairs and associated rewards) to iteratively improve their estimates of the optimal policy or value function. ============================================
|
||||||||
| ================================================================================= | ||||||||
|
|
||||||||

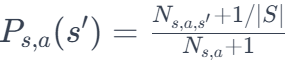 ------------------------ [3676al]
------------------------ [3676al]