Laplace Smoothing/Laplace Correction/Add-One Smoothing - Python and Machine Learning for Integrated Circuits - - An Online Book - |
||||||||
| Python and Machine Learning for Integrated Circuits http://www.globalsino.com/ICs/ | ||||||||
| Chapter/Index: Introduction | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Appendix | ||||||||
================================================================================= When working with probabilistic models or Bayesian classifiers, Bayes' theorem below is used for making predictions in binary classification, where,:
It is used to estimate the probability of an example belonging to a specific class, typically class 1 (y=1), based on the observed features (x). Adding 1 to the numerator and 2 to the denominator is a technique used to handle cases where you have very limited data and want to avoid division by zero or extreme probabilities in a Bayesian setting. This is known as Laplace smoothing, Laplace correction, or add-one smoothing, and it's commonly used when dealing with small sample sizes in probability calculations. The idea behind Laplace smoothing is to provide a small, non-zero probability estimate for events that have not been observed in the data. This is particularly useful in Bayesian statistics and probabilistic models to avoid situations where you have zero counts in your data, which can lead to problematic calculations. In this case, Equation 3833a becomes, This smoothing helps avoid the problem of division by zero when you have zero counts for certain events or features in your data. By adding 1 to the numerator and 2 to the denominator, you ensure that you always have a non-zero probability estimate for each event, even if you haven't observed it in your data. This can lead to more stable and interpretable probability estimates, especially when you have limited data. Laplace smoothing is a common technique in machine learning and statistics to handle issues related to sparse data and avoid extreme probabilities that can arise when working with small datasets. Table 3833. Applications of Laplace smoothing.
============================================
|
||||||||
| ================================================================================= | ||||||||
|
|
||||||||
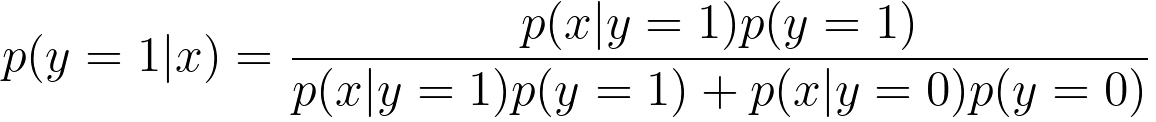 -------------------------------- [3833a]
-------------------------------- [3833a]