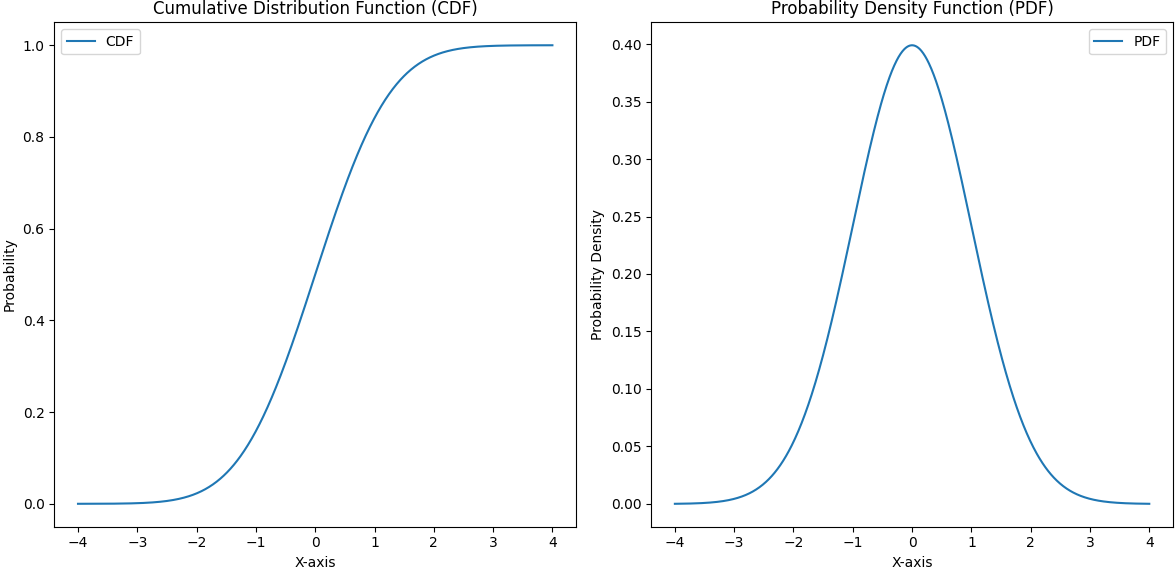
=================================================================================

In machine learning, the term "cumulative" in the Cumulative Distribution Function (CDF) refers to the accumulation or summing up of probabilities as we move along the range of possible values of a random variable. CDF F(x) of a random variable X is a function that gives the probability that the random variable X is less than or equal to a certain value x given by,

          ---------------------------------------- [3688a]

The CDF properties are:

          i) 0 ≤ F(x) ≤ 1 for all x ---------------------------------------- [3688ah]

          ii) F(x) is non-decreasing, meaning that as x increases, F(x) does not decrease.

          iii) The limit of F(x) as x approaches negative infinity is 0, and the limit as x approaches positive infinity is 1.

The CDF can be used to analyze and understand the distribution of a random variable. It is particularly useful when dealing with continuous random variables. The probability density function (PDF) is often associated with the CDF, and they are related by the derivative,

          ---------------------------------------- [3688b]

where,

         f(x) is the probability density function.

CDF is used in feature engineering, data analysis, and model evaluation. It provides insights into the distribution of data and helps in making informed decisions about how to handle different aspects of a machine learning problem.

Figure 3688 shows the comparison between cumulative distribution function and probability density function.

Figure 3688. Comparison between cumulative distribution function and probability density function (code).

============================================