Posterior Probability versus Prior Probability - Python and Machine Learning for Integrated Circuits - - An Online Book - |
||||||||||||||||||
| Python and Machine Learning for Integrated Circuits http://www.globalsino.com/ICs/ | ||||||||||||||||||
| Chapter/Index: Introduction | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Appendix | ||||||||||||||||||
================================================================================= Posterior probability and prior probability are fundamental concepts in probability theory and Bayesian statistics. Table 3836 lists the comparison between posterior probability and prior probability. Table 3836. Posterior probability and prior probability.
For instance, when working with probabilistic models or Bayesian classifiers, Bayes' theorem below is used for making predictions in binary classification, where,:
It is used to estimate the probability of an example belonging to a specific class, typically class 1 (y=1), based on the observed features (x). For a specific case study, assume we're working on a binary classification problem where we want to predict whether an email is spam (class 1) or not spam (class 0) based on the presence or absence of two words: "money" and "lottery." We'll calculate the probability that an email is spam (y=1) given the observed words (x) using Equation 3836a. Let's assume the following probabilities:
Now, let's consider the probabilities of observing the words "money" and "lottery" in both spam and non-spam emails:
Now, suppose you receive an email that contains both "money" and "lottery" (x = ["money", "lottery"]). You want to determine whether this email is spam (y=1) or not (y=0). Using Equation 3836a, substituting the probabilities: Then, the posterior probability p(y=1|x), which represents the probability that the email is spam (class 1) given the observed words "money" and "lottery.", is equal to 6. Therefore, the probability that this email is spam (y=1) given the words "money" and "lottery" is 6 times higher than it being not spam (y=0). In this case, you would predict that the email is likely spam. This is a simplified example, but it demonstrates how the formula can be used to calculate class probabilities in a binary classification scenario. In this example above, p(y =1|x) is the probability you want to compute after considering the evidence (the words "money" and "lottery"), while p(y=1) is your initial belief about the probability of an email being spam. In Bayesian statistics, the equation on the updated probability distribution of parameters or hypotheses, which represents the updated probability distribution of parameters or hypotheses based on observed data, can be given by, P(θ|D) ∝ P(D|θ) * P(θ) ---------------------------------- [3836c] where:
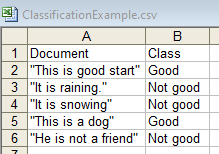
Next example is to find which class, for a document, maximize the posterior possibility with Bayes' Theorem: where, word1, word2, word3, ..., wordn are the words in the particular document. If there are too many words in the documents, then we can make two assumptions: i) Word order does not matter, so we use BOW representations. ii) Word appearances are independent of each other given a particular class. This is why "Naive" comes from. However, in real life, some words, e.g. "Thank" and "you" are correlated. The Naive Bayes Classifier is given by the log formula below, For instance, a csv file has contents below: Then, the Priors, P(c) are: P(Good) = 2/5 P(Not good) = 3/5 ============================================
|
||||||||||||||||||
| ================================================================================= | ||||||||||||||||||
|
|
||||||||||||||||||

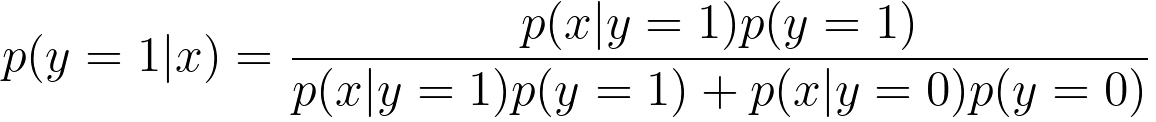 -------------------------------- [3836a]
-------------------------------- [3836a] 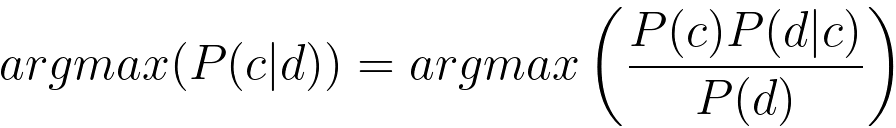 ------------------------ [3836d]
------------------------ [3836d] 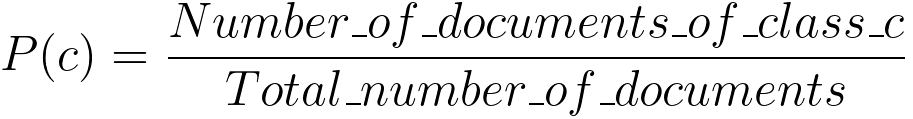 -------------- [3836e]
-------------- [3836e] 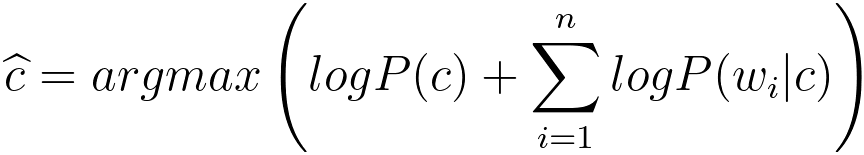 --------------------------- [3836h]
--------------------------- [3836h]