=================================================================================
Electron diffraction patterns and Kikuchi patterns in both EBSD and CBED present similar geometry and can be successfully calculated using a Bloch-wave approach. The Bloch-wave is known from Bloch’s theorem for a translationally invariant scattering potential,
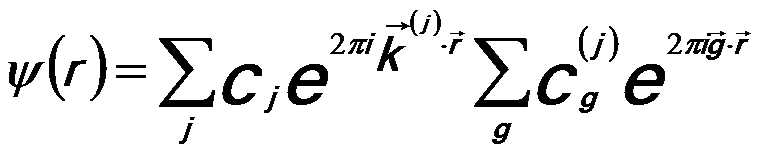 ------------------- [2208a] ------------------- [2208a]
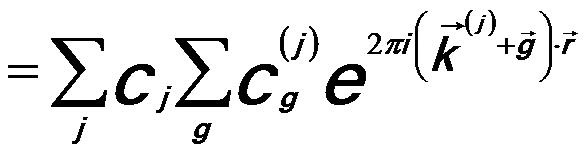 ------------------- [2208b] ------------------- [2208b]
where,
cj and cg(j) -- Coefficients;
k(j) -- Vectors.
These coefficients and vectors can be obtained by solving Schrödinger equation by limiting the wave-function expansion to a number of Fourier coefficients labeled by the respective reciprocal lattice vectors g, coupling the incident electron beam to a diffracted beam. The eigenvalues λ(j) is obtained by re-writing the Bloch-wave vector k(j) as the sum of the incident beam wave vector K in the crystal and a surface normal component as k(j) = K + λ(j)n. Equation 2208b can be re-written by,
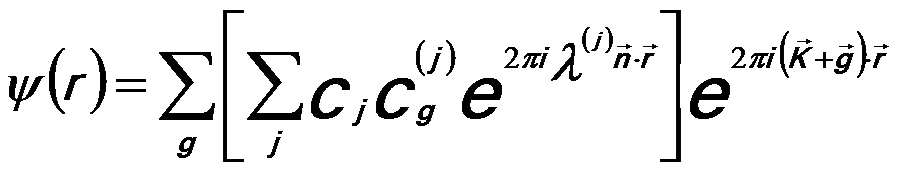 ------------------- [2208c] ------------------- [2208c]
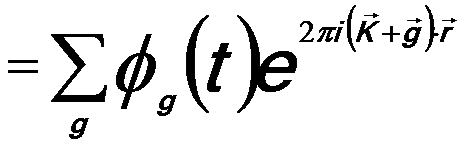 ------------------- [2208d] ------------------- [2208d]
where,
t – The depth from the entrance surface of the sample.
The exponential term exp[2πi(K + g)·r] in Equation 2208d indicates the contributions of plane waves moving into the directions K + g. ϕg(t) gives the a depth dependent amplitude. The plane waves in directions K + g correspond to the diffracted beams that form a spot diffraction pattern.
|
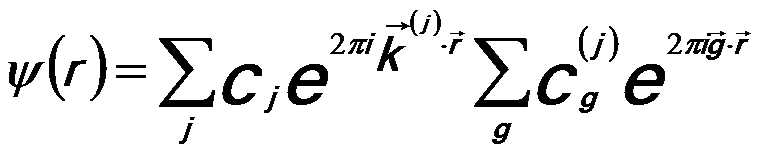 ------------------- [2208a]
------------------- [2208a] 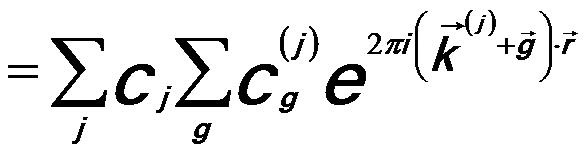 ------------------- [2208b]
------------------- [2208b] 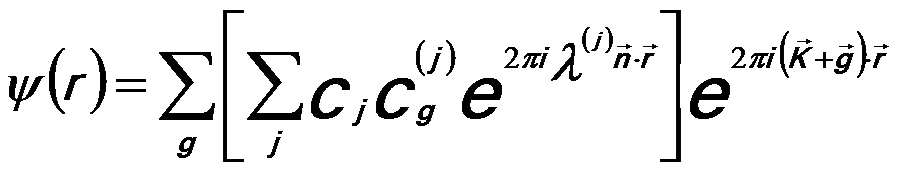 ------------------- [2208c]
------------------- [2208c] 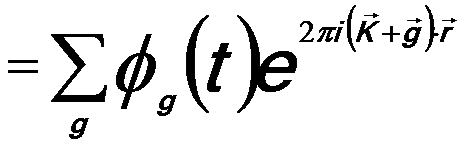 ------------------- [2208d]
------------------- [2208d]