=================================================================================
Based on band theory, when a large number of atoms combine to form a large aggregate, molecular orbitals merge into an almost continuous band of energy levels. The bottom half (called valence band) of the band is composed of bonding M.O.s (molecular orbitals) and is filled with electrons. The upper half (called conduction band) of band is composed of antibonding M.O.s and is empty.
The valence band electrons normally originate from the electrons in the incomplete outer shell of atoms, for instance, the valence band is formed for silicon (Si) crystals as shown in Figure 2632a. An isolated Si atom contains 14 electrons, which occupy 1s, 2s, 2p, 3s and 3p orbital in pairs. When atoms are far away from each other, the electrons in the out shell do not interact. As the distance between atoms is reduced to d1, there is an overlap of electron wavefunctions across adjacent atoms. This leads to a splitting of the energy levels consistent with Pauli exclusion principle, and forming energy bands. This splitting leads to 2N states in the 3s band and 6N states in the 3p band, where N is the number of Si atoms in the crystal. A further reduction of the lattice spacing causes the 3s and 3p energy bands to merge into a single band having 8N available states, and then split again into two bands containing 4N states each. At the temperature of zero Kelvin, the lower band is completely filled with electrons and named as the valence band. The upper band is empty and named as the conduction band. Note that in crystal Si (with lattice spacing d0), the core level electrons do not start yet to interact.
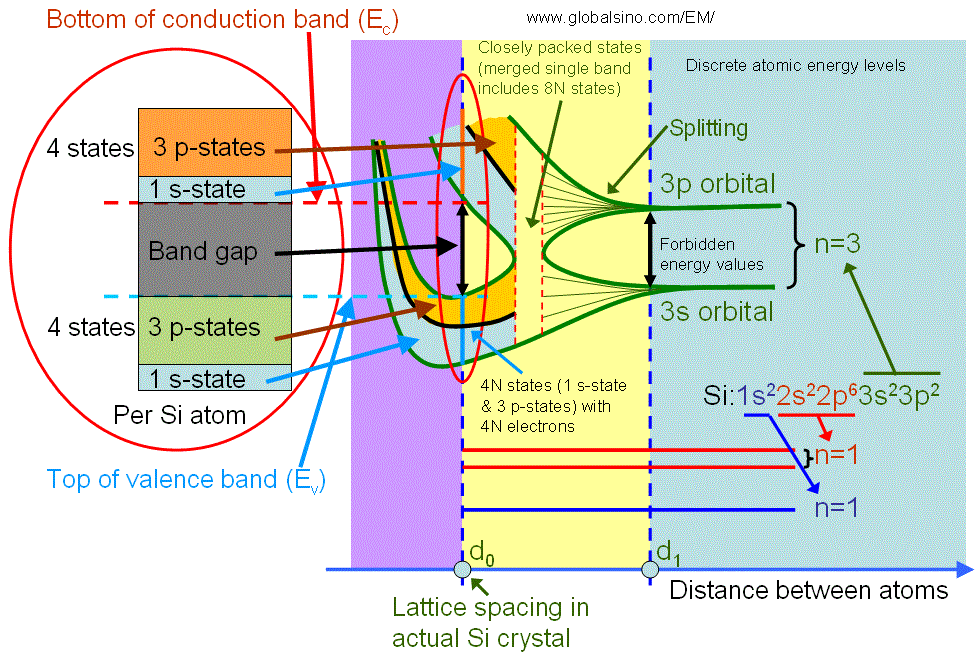
Figure 2632a. Detailed illustration of electronic structure of silicon as a function of distance between atoms. The left red circle is a zoom-in of the right red circle.
Figure 2632b shows the schematic illustration of the energy level diagrams for molecular structures with different number of atoms which are single atoms, dimers, clusters and bulk materials. Splitting of the atomic energy levels occurs when the single atoms form a diatomic molecule. As more atoms join the system, the levels split further until a quasi-continuous band structure is formed in the bulk material. In other words, quantum size effects occur when the quasi-continuous band structure of a solid state system begins to break down as more atoms are included.
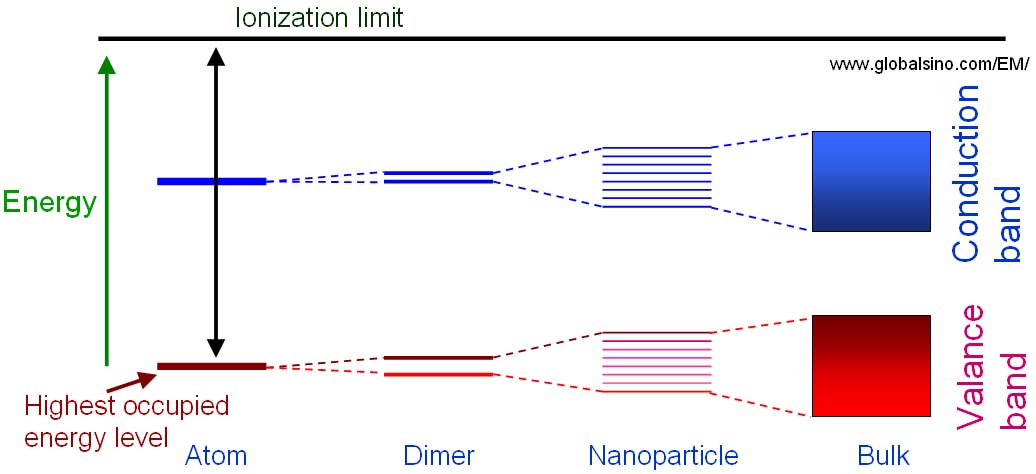
Figure 2632b. Schematic illustration of the energy level diagrams for molecular structures with different number of atoms which are single atoms, dimers, clusters and bulk materials.
For instance, the schematic illustration in Figure 2632c shows the bonding levels for diamond and indicates the formation of conduction band. When the hybrid carbon atoms bond, a second electron is contributed to the state by the other atom, and thus the interaction between the two electrons lowers the energy of the state. Therefore, the sp3 energy level splits into a series of four bonding and four antibonding orbitals. In an actual solid, there is a Coulomb interaction between the atom cores and the electrons, and then the bonding and anti-bonding energy levels split to form a continuous band structure, with the band of bonding states being the valence band and the anti-bonding states being the conduction band.
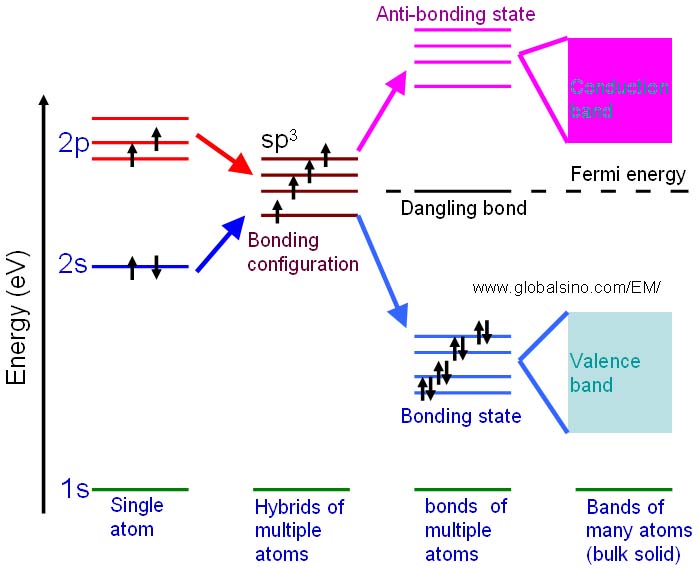
Figure 2632c. Schematic illustration showing the progression of the electronic structure for an sp3 bonded system.
However, in some materials, those electrons in different orbitals form their own energy levels of valence and conduction bands as shown in Figure 2632d.
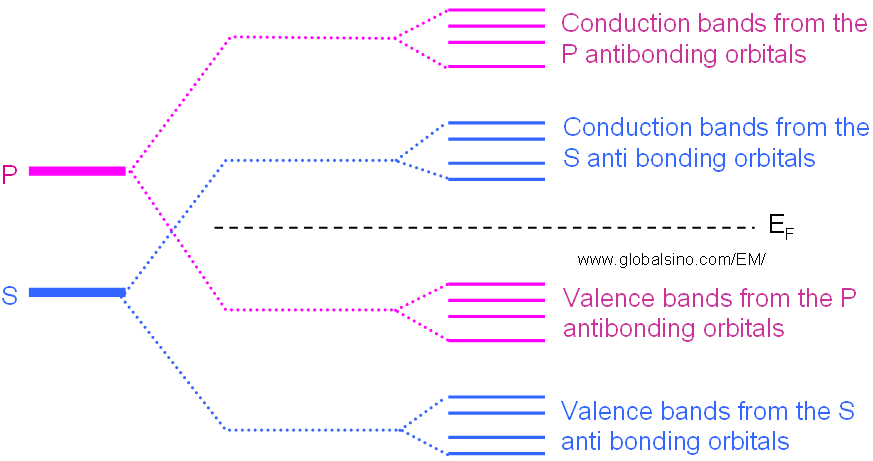
Figure 2632d. Schematic illustration of evolution of the atomic s and p orbitals into valence and conduction bands in some materials.
Figure 2632e shows an example of the ionization processes and generations of X-rays. A high-energy electron (incident electron) must penetrate through the outer conduction/valence bands and interact with the inner-shell (or core) electrons. If the high-energy electron transfers more than a critical amount of energy to an inner-shell electron (K electron here), that electron is ejected into the vacuum, that is, it escapes (step 2b in the figure) the attractive field of the nucleus, leaving a hole in the inner shell (K shell in the figure) and escapes above the Fermi level into the unfilled states. In this case, the atom is ionized. The excited atom can return almost to its ground state (lowest energy) by filling in the hole with an electron from an outer shell (step 3). This transition is accompanied by the emission of an X-ray in Figure 2632e. The energy of the X-ray emission is characteristic of the difference in energy between the two electron shells involved (L3 → K in the figure) and this energy difference is unique to the specific atom.
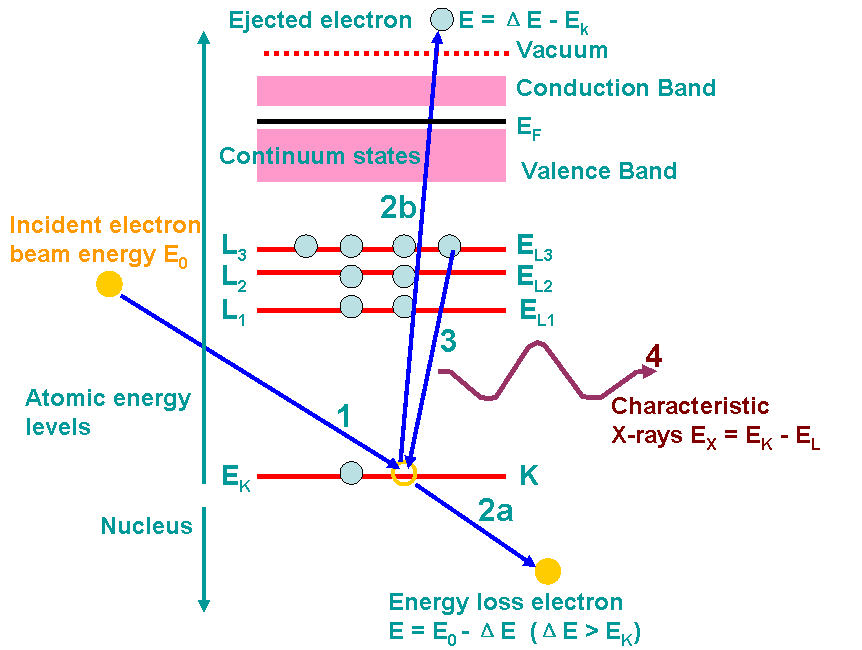
Figure 2632e. Example of the ionization processes and generations of X-rays. The numbers indicates the process sequence. In this process, an inner (K) shell electron is ejected
from the atom by a high-energy electron (incident electron). In step 3, the hole in the K shell
is filled by an electron from the L shell (L3 here), characteristic (Kα) X-ray emission
occurs (step 4). The beam electron loses energy but continues on through the
specimen (step 2a). Steps 2a and 2b almost occur at the same time.
The gap between the top of valence band and the bottom of conduction band is defined as energy gap Eg. In insulators, the energy gap is very large and no vacant conduction band is available to the valence electrons. Otherwise, the energy gap is either zero due overlapping between valence and conduction bands for metals or is very small for semi-conductors so that conduction band is easily available to valence electrons.
|



