This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
 

=================================================================================

In TEM analysis, the probability of an incident electron interacting with an atom as it penetrates through a specimen can be described in terms of "cross section" (σ) and "mean free path" λ. The mean free path represents how thin the specimen needs to avoid or minimize plural scatterings. These scatterings involve both elastic and inelastic scatterings of electrons. For the simplified case with specimen thickness t, which consists of N atoms/unit volume, and where other effects (e.g. electron cloud screening) are ignored, the total probability of scattering an electron as it penetrates through the specimen is, in terms of mean free path, given by,

          1/λ = N_Aσ_T(ρt)/A ---------------------------------------- [2865a]
where,
          N_A -- Avogadro's number,
          σ_T -- The total scattering cross sectoin (including both elastic and inelastic scatterings, i.e. σ_elastic + σ_inelastic) for an isolated atom,
          ρ -- The mass density,
          A -- The atomic weight of the atoms in the specimen which have a density of ρ and mass-thickness of ρt.

If diffraction effects are negligible then the normalized scattering intensity I/I₀ can be given by, [1]

         I/I₀ = 1 − exp(−t/λ) -------------------------- [2865b]
where,
         λ -- The mean free path of the scattering.

The cross-section of the scattering can be extracted by the relation,
         1/λ = Nσ -------------------------- [2865c]
where,
         N = ρ/(A_dm_p)
         N -- The atomic density,
         A_d -- The dimensionless atomic mass,
         m_p -- The proton mass.

Figure 2865 shows the experimental values of λ_el [3] and λ_in(Z) [2] as oscillatory functions of Z for Z > 20. Comparison of λ_el and λ_in values suggests that the elastic component should dominate scattering of incident high-energy electrons for most inorganic solids and of incident electrons penetrating thin TEM specimens. The figure also indicates λ_el ≤ λ_in.

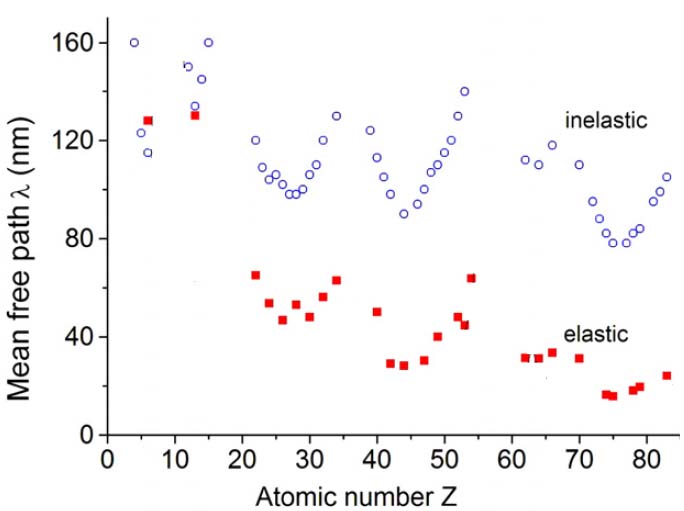
Figure 2865. The mean free path of elastic scattering λ_el of 200 keV electrons (solid squares) [3] and that of inelastic values λ_in (open circles) (Adapted from [2]).

[1] Egerton R. F., 1996, Electron Energy Loss Spectroscopy in the Electron Microscope (New York: Plenum).
[2] Iakoubovskii K, Mitsuishi K, Nakayama Y and Furuya K (2008) Phys. Rev. B 77, 104102.
[3] Konstantin Iakoubovskii and Kazutaka Mitsuishi, Elastic scattering of 200 keV electrons in elemental solids: experimental observation of atomic-number-dependent oscillatory behavior, J. Phys.: Condens. Matter 21 (2009) 155402.