=================================================================================
The EEL spectrum can be described in a dielectric formulation [1] by,
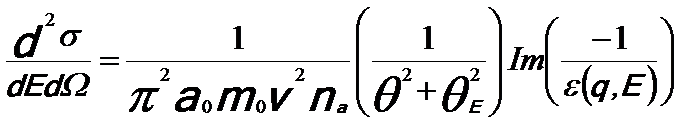 -------- [3372a] -------- [3372a]
where,
v -- The speed of the incident electron;
na -- The number
of atoms per unit volume;
θE -- The characteristic scattering angle (θE = E/γm0v2);
Im(−1/ε) -- The energy loss function
Based on Equation 3372a and a Kramers–Kronig analysis, the complex dielectric function ε = ε1 + iε2 can be obtained from the low-loss EEL spectrum. Furthermore, with approximation, it can be obtained,
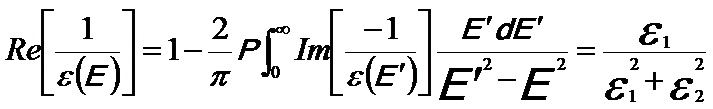 -------- [3372b] -------- [3372b]
The TEM specimen thickness can be extracted using Kramers-Kronig sum rule, [2, 3]
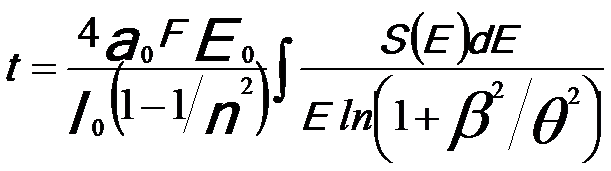 -------- [3372c] -------- [3372c]
where,
a0 -- The Bohr radius,
E0 -- The electron energy,
F -- The
relativistic factor,
n -- The optical refractive index,
β -- The
collection angle,
θ ≈ E/(2FE0).
Experimental tests revealed that the thickness calculation by Kramers-Kronig sum rule is accurate to ~10%. [2,3]
The optical absorption α can be given by,
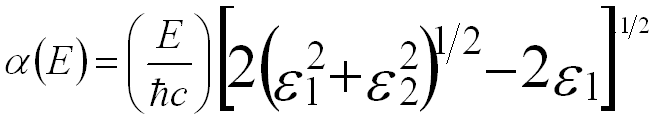 -------- [3372d] -------- [3372d]
As discussed on page4360, the energy-loss process of incident electrons can be treated by the dielectric response of the electrons. Therefore, the EELS contains information about the dielectric constant ε. The single-scattering spectrum intensity I is given by,
I = I0(t/k)Im(-1/ε)ln[1 + (β/θE)2] --------------------------------- [3372e]
where,
I0 -- The intensity in the zero-loss peak.
t -- The specimen thickness.
k – A constant incorporating the electron momentum and Bohr radius.
Note that if the SSD is known, then optical
techniques such as Kramers–Kronig analysis can be
applied to determine the dielectric function, reflectivity,
absorption, etc. [1]
Figure 3372a shows the EEL spectra of plasmon region (zero-peak is not shown) for crystalline and amorphous diamond. The loss function (Im[-l/ε]) can then be obtained by removing contribution from multiple scattering using the Fourier-log deconvolution method.
Figure 3372a. EEL spectra of plasmon region for (a) crystalline and (b) amorphous diamond.
An optical absorption method (see Equation 3372d) can directly provide the imaginary part of the dielectric function, ε2, associated with a single electron excitation of an interband transition, while EELS cannot directly give ε2. Based on the obtained loss function, the real part (ε1), and the imaginary part (ε2) of the dielectric function for the crystalline and the amorphous diamond are extracted using Kramers-Kronig analysis as shown in Figure 3372b. Table 3372 lists the onset energy (indicating the band gap energy) and the peaks in the imaginary spectrum obtained from Figure 3372b and the original interband transitions. In many cases, the broad maxima in ε2, e.g. with energies higher than 10 eV, represent widely distributed oscillator strengths. That is, the peaks in ε2 correspond to some interband transitions.
Figure 3372b. Real part (ε1), and the imaginary part (ε2) of the dielectric function for (a) crystalline and (b) amorphous diamond.
Table 3372. Onset energies (band gap energies), peaks in the imaginary spectrum in Figure 3372b and the original interband transitions.
| |
Onset energy (band gap energy) |
Peaks in imaginary spectrum |
Interband transition |
Crystal diamond |
5.5 eV |
8.2 |
Γ point |
| 12.7 |
X and L points |
Amorphous diamond |
4.0 eV |
7.2 eV |
Γ point |
[1] R. F. Egerton, Electron Energy Loss Spectroscopy in the Electron Microscope, Plenum Press, New York, (1996).
[2] Y. Y. Yang and R. F. Egerton, Micron 26, 1 (1995).
[3] R. F. Egerton and S. C. Cheng, Ultramicroscopy 21, 231 (1987).
|