|
|
Transition Probability from Initial State to Final State
- Practical Electron Microscopy and Database -
- An Online Book -
|
|
https://www.globalsino.com/EM/
|
|
This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
|
=================================================================================
Fermi’s Golden Rule is also referred to as the Golden Rule of time-dependent perturbation theory, which provides a way to evaluate the transition rate between two certain quantum-mechanically defined states (namely, initial state and final state). The transition rate depends on the strength of the coupling between the two states of the system as well as on the number of ways that the transition can happen (i.e., the density of the final states). In many physical situations the transition probability is given by,
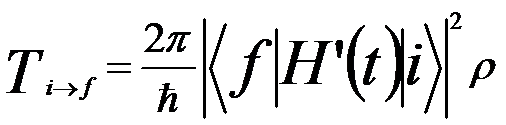 -------------------- [3796] -------------------- [3796]
where,
ρ -- The density of the final states (e.g. the number of states per unit of energy)
H'(t) -- The time-dependent perturbation, e.g. corresponding to the interaction of the electron plane wave with an atom in EMs
<f|H'(t)|i> -- The matrix element of the perturbation H'(t) between the final and initial states.
This transition probability is sometimes called decay probability and is related to mean lifetime. Due to the generality of Fermi’s Golden Rule, this principle has various applications in the field of atomic, nuclear, and solid-state physics. In a scattering process, Fermi's golden rule is valid when the initial state has not been significantly depleted by scattering into the final states.
|
=================================================================================
The book author (Dr. Liao) welcomes your comments, suggestions, and corrections, please click here for submission. You can click How to Cite This Book to cite this book. If you let Dr. Liao know once you have cited this book, the brief information of your publication will appear on the “Times Cited” page. This appearance can help advertise your publication.
|
|
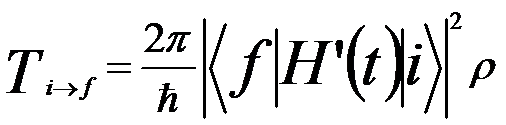 -------------------- [3796]
-------------------- [3796]