=================================================================================
As we know that in TEM observation, the transmission of unscattered incident electrons is inversely proportional to the TEM specimen thickness. On the other hand, the increase of the specimen thickness enhances the energy loss of the transmitted electrons. Therefore, the spatial resolution degrades with the increase of specimen thickness because of the chromatic aberration effects. Table 4265 lists examples of the energy loss of incident electrons passing through the specimen. The use of thinner specimen can generally improve spatial resolution because it minimizes the energy loss.
Table 4265. Examples of the energy loss of electrons passing through the TEM specimen.
| |
Accelerating voltage of incident electrons |
Penetrated electrons (%) |
Penetrated electron with energy loss higher than 50 eV (%) |
Unscattered electrons (%) |
Elastically scattered electrons (%) |
| Thin metal foil |
|
50 |
40 |
|
|
| 50 nm thick carbon film |
50 kV |
|
55 |
33 |
10 |
Similar to the discussion regarding different accelerating voltages (the focal length at low accelerating voltages is much smaller than that at high accelerating voltages), for chromatic aberration, the light or electrons of different wavelength (or different energy E) are focused differently as shown in Figure 4265. Different color represents different wavelength or energy of rays (light or electrons). There exists a point called the circle of least confusion, where chromatic aberration can be minimized and where the image plane locates.
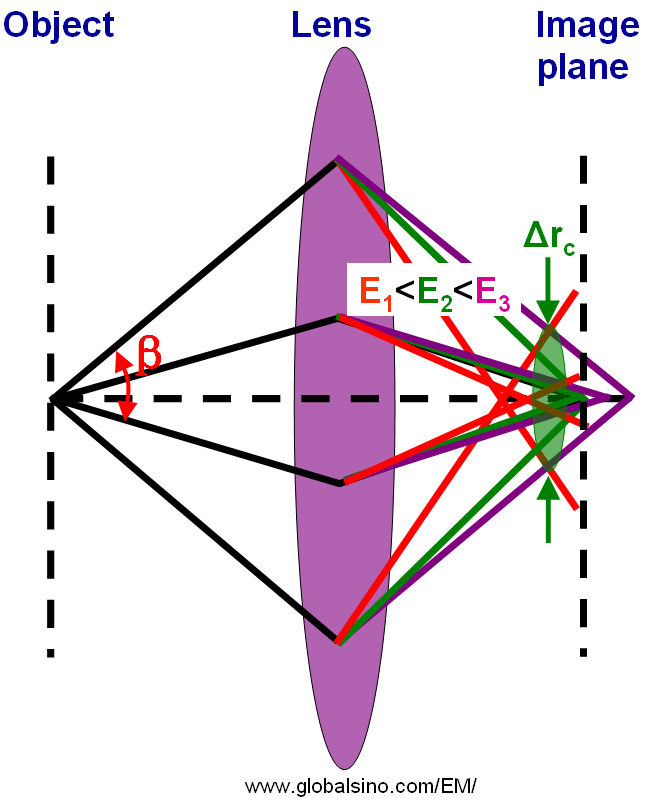
Figure 4265. Schematic diagram of chromatic aberration.
In the case of chromatic aberration, the radius (Δrc) of the circle of least confusion can be given by,
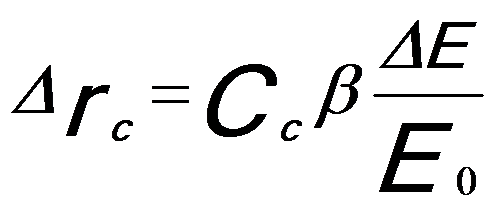 --------------------- [4265a] --------------------- [4265a]
The Cc coefficient is approximately equal to the focal length.
Equation 4265a indicates that the image of a single point will be a disk in the radius of Δrc, which limits the spatial resolution of the microscope.
|

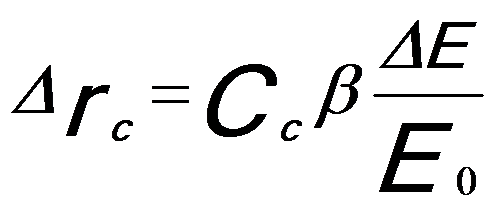 --------------------- [4265a]
--------------------- [4265a]