=================================================================================
For elastic scattering, based on theories of conservations of energy and momentum and electron interaction with single atomic nucleus, the appreciable energy (ΔE) transferred to an atom by an electron scattered through scattering angle θ is given by,
ΔE = Emax sin2(θ/2) ------------------------------------------- [4753a]
where Emax is the maximum possible energy transfer to be determined from relativistic kinematics [1], given by,
Emax = E0(1.02 + E0/106)/(465.7·A) ----------------------- [4753b]
where, A -- Atomic mass
number
E0 -- Incident-electron energy (in eV)
Two extreme cases are:
i) ΔE ≈ 0 (<< 1 eV, which may not be detectable by EELS), for small angle (θ≈ 0)
ii) ΔE = several eV, for high angle. For instance, for the extreme case of 180° backscattering, ΔE = Emax ≈ 18 eV for a carbon atom and E0 = 100 keV. [2]
For TEM (transmission electron microscope), the primary electron beam typically with voltages of 100 to 300 keV at convergence half angle α interacts with a specimen sufficiently thin as shown in Figure 4753. An aperture (e.g. objective aperture) defines at the level of the specimen a solid angle of collection (acceptance half angle β of a few mrad). During this interaction, the occurred scattering events provide the information of momentum transfer q and of energy transfer ΔE.
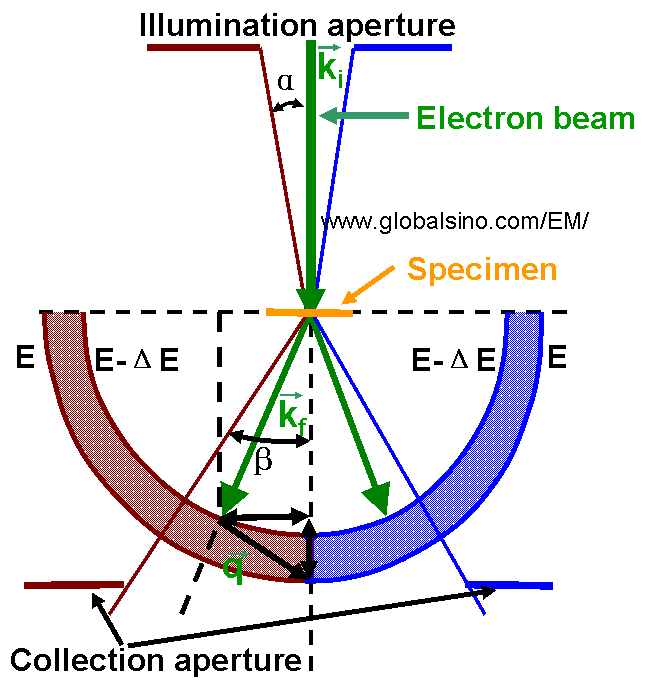
Figure 4753. Schematic diagram showing wave vector ki of incident electron, scattered electron
wave vector kf, transferred wave vector q, and energy transfer ΔE.
[1] R. F. Egerton, F. Wang, and P. A. Crozier, Microsc. Microanal. 12, 1 (2006).
[2] R. F. Egerton, Electron energy-loss spectroscopy in the TEM, Rep. Prog. Phys. 72 016502 (2009).
|
