According to Bragg Condition of electron elastic scattering, the reciprocal space vector q (nm-1) in reciprocal space in an electron microscope (e.g TEM and STEM) follows the small-angle Bragg
law,
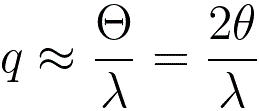 -------------------------------- [1196] -------------------------------- [1196]
where,
Θ -- The total scattering angle (in rad) between the incident and scattered beam,
θ -- The
Bragg angle (in rad), (see page3882)
λ -- The electron wavelength at a specific acceleration voltage (nm). (see page4787)
Based on Equation 1196, Table 1196 can be obtained.
| Table 1196. Conversion between reciprocal space vector and angle at different accelerating voltages. 1 rad = 1000 mrad. |
Angle (Θ) |
Reciprocal space vector (q, nm-1) |
(mard) |
(degree, °) |
10 keV |
50 keV |
80 keV |
100 keV |
200 keV |
300 keV |
400 keV |
| 5 |
0.3 |
0.4 |
0.9 |
1.2 |
1.3 |
2.0 |
2.5 |
3.0 |
| 10 |
0.6
|
0.8 |
1.9 |
2.4
|
2.7 |
4.0 |
5.1 |
6.1 |
| 20 |
1.1 |
1.6 |
3.7 |
4.8 |
5.4 |
8.0 |
10.2 |
12.2 |
| 30 |
1.7 |
2.5 |
5.6 |
7.2 |
8.1 |
11.9 |
15.2 |
18.3 |
| 40 |
2.3 |
3.3 |
7.5 |
9.6 |
10.8
|
15.9 |
20.3 |
24.3 |
| 50 |
2.9 |
4.1 |
9.3 |
11.9 |
13.5
|
19.9 |
25.4 |
30.4 |
| 60 |
3.4 |
4.9 |
11.2 |
14.3 |
16.2
|
23.9 |
30.5 |
36.5 |
| 70 |
4.0 |
5.7 |
13.0 |
16.7 |
18.9 |
27.9 |
35.5 |
42.6 |
| 80 |
4.6 |
6.5 |
14.9 |
19.1 |
21.6 |
31.9 |
40.6 |
48.7 |
| 90 |
5.2 |
7.4 |
16.8
|
21.5 |
24.3 |
35.8 |
45.7 |
54.8 |
| 100 |
5.7 |
8.2 |
18.6 |
23.9 |
27.0 |
39.8 |
50.8 |
60.8 |
| 110 |
6.3 |
9.0 |
20.5 |
26.3 |
29.7 |
43.8 |
55.8 |
66.9 |
| 120 |
6.9 |
9.8 |
22.4 |
28.7 |
32.4 |
47.8 |
60.9 |
73.0 |
| 130 |
7.5 |
10.6 |
24.2 |
31.1 |
35.1 |
51.8 |
66.0 |
79.1 |
| 140 |
8.0 |
11.4 |
26.1 |
33.5 |
37.8 |
55.8 |
71.1 |
85.2 |
| 150 |
8.6 |
12.3 |
27.9 |
35.8 |
40.4 |
59.7 |
76.2 |
91.3 |
| 160 |
9.2 |
13.1 |
29.8 |
38.2 |
43.1 |
63.7 |
81.2 |
97.3 |
| 170 |
9.7 |
13.9 |
31.7 |
40.6 |
45.8 |
67.7 |
86.3 |
103.4 |
| 180 |
10.3 |
14.7 |
33.5 |
43.0 |
48.5 |
71.7 |
91.4 |
109.5 |
| 190 |
10.9 |
15.5 |
35.4 |
45.4 |
51.2 |
75.7 |
96.5 |
115.6 |
| 200 |
11.5 |
16.3 |
37.3 |
47.8 |
53.9 |
79.7 |
101.5 |
121.7 |
|