There are three symmetry elements which define the point group of a crystal:
i) The roto-inversion axes (-X). The symmetry operation of roto-inversion is obtained with rotation by 360/n about an axis, followed by inversion through a point.
ii) The X-fold rotation axes.
iii) The mirror planes of symmetry. A mirror (m) is equivalent to -2.
Hermann-Mauguin (H-M) System is usually referred to as the International System since it has been used most frequently in crystallographic analysis. Some conventional "rules" for the symbols (names) of the point groups are used with the H-M notation:
i) For the groups only with one two-fold axis, one mirror, or one inversion center, their notations can be only one symbol, e.g. 1 and -1 triclinic crystal system.
ii) If the symbol for the group contains three positions, then they denote symmetry elements in the X, Y, Z directions, respectively.
iii) For the groups with one higher-order axis than three axes, the primary direction (e.g. Z direction) with the high-order axis uses the first position. The symmetrically equivalent secondary directions that use the second position are perpendicular to Z-axis. The symmetrically equivalent tertiary directions use the third position. From instance, the short symbol for 4/m 2/m 2/m (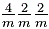 ) is 4/mmm ( ) is 4/mmm (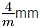 ), but cannot be mmm. ), but cannot be mmm.
iii.a) For the groups with odd-order axes n and -n, the third position in symbol is always absent, because all the n directions, perpendicular to higher-order axis, are symmetrically equivalent. For instance, all the three mirror planes (m0, m1, m2) in Figure 1623a are equivalent. All of them pass through one vertex and the center of the opposite side.
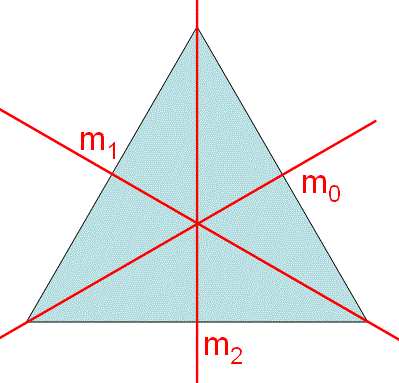
Figure 1623a. Mirror planes (m0, m1, m2) of a triangle.
iii.b) For the groups with even-order axes n and -n, there are n/2 secondary directions and n/2 tertiary directions. For instance, there are two sets of mirror planes (i.e. three planes go through two opposite vertexes in red, and three other planes go though the centers of opposite sides in blue) in the hexagon in Figure 1623b. In this case, any of the two sets can be selected as secondary directions, and the other set will be tertiary directions. Therefore, -42m, -62m and -82m can be written as -4m2, -6m2 and -8m2.
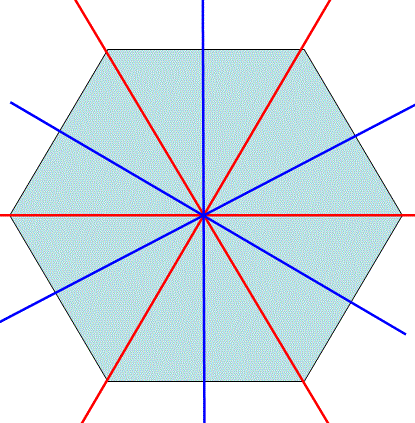
Figure 1623b. Mirror planes of a hexagon.
iv) For the groups with several high-order axes, for instance, a cubic crystal system has four diagonal 3-fold axes, directed along its four space diagonals. The first position of the symbols of such groups is given to the symmetrically equivalent directions of the coordinate axes X, Y, Z. The second position is assigned to the diagonal 3 or -3 axes. The third position is assigned to the diagonal directions between any two of the three coordinate axes X, Y, and Z.
v) For many point groups, if the rotation axis can be unambiguously obtained from the combination of symmetry elements presented in the symbol, the n-fold rotation axes in n/m positions can then be ignored. From instance, the short symbol for 2/m 2/m 2/m (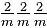 ) is mmm, for 4/m 2/m 2/m ( ) is mmm, for 4/m 2/m 2/m (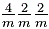 ) is 4/mmm ( ) is 4/mmm (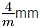 ), and for 4/m -3 2/m ( ), and for 4/m -3 2/m (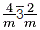 ) is m-3m. ) is m-3m.
Table 1623 lists the notations of the 32 crystallographic point groups. The Schoenflies notation system has nomally been used to describe the symmetry of molecules. The different conventions for all the crystal systems are given in the International Tables.
Table 1623. Notations of the 32 crystallographic point groups (also see page1677).
| Crystal system |
Hermann-Mauguin notation |
Schoenflies notation |
Hermann-Mauguin notation |
Characteristics |
Remarks |
| Triclinic |
1 |
C1 |
|
|
| -1 |
Ci |
|
|
| Monoclinic |
2 |
C2 |
|
|
| m |
Cs |
|
|
| 2/m |
C2h |
|
A twofold axis parrallel to the normal to a mirror plane. |
| Orthorhombic |
222 |
D2 |
The three symbols refer to the three orthogonal axes. |
|
| mm2 |
C2v |
Mirrors normal to x and y with a twofold axis along z. |
| mmm |
D2h |
|
| Tetragonal |
4 |
C4 |
|
|
| -4 |
S4 |
|
|
| 4/m |
C4h |
|
|
| 422 |
D4 |
|
|
| 4mm |
C4v |
|
|
| -42m |
D2d |
|
|
| 4/mmm |
D4h |
|
|
| Trigonal |
3 |
C3 |
|
Has a three-fold rotation symmetry |
| -3 |
C3i |
|
Has a three-fold roto-inversion symmetry |
| 32 |
D3 |
|
|
| 3m |
C3v |
|
|
| -3m |
D3d |
|
|
| Hexagonal |
6 |
C6 |
|
|
| -6 |
C3h |
|
|
| 6/m |
C6h |
|
|
| 622 |
D6 |
|
|
| 6mm |
C6v |
|
|
| -62m |
D3h |
|
|
| 6/mmm |
D6h |
|
|
| Cubic |
23 |
T |
The first symbol: the cube axes; the second symbol: always 3 (or -3), representing the cubic system and refering to the body diagonals; the third symbol: the face diagonals. |
|
| m-3 |
Th |
|
| 432 |
O |
|
| 4-3m |
Td |
|
| m-3m |
Oh |
|
X: Major X-fold rotation axis alone, including 1, 2, 3, 4, and 6.
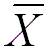 : Inversion axis alone, namely, the major X-fold inversion axes, including -1, -2, -3, -4, and -6. : Inversion axis alone, namely, the major X-fold inversion axes, including -1, -2, -3, -4, and -6.
m: The direction normal to the mirror plane (equivalent to -2)
X/m: Rotation axis with a symmetry plane normal to it.
Xm: Rotation axis with a symmetry plane that is not normal to it (usually a vertical symmetry plane).
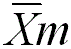 : Inversion axis with a symmetry plane not normal to it. : Inversion axis with a symmetry plane not normal to it.
X⊥2: Rotation axis with a diad normal to it (The two-fold rotation axis is perpendicular to the major axis).
/: Parallel symmetry elements.
X/mm: Rotation axis with a symmetry plane normal to it and another not so. |
The symbols for symmetry elements of space groups are more diverse than those for point groups, because in addition to rotation axes and mirror planes, a space group may contain more complex symmetry elements, i.e. screw axes (combination of rotation and translation) and glide planes (combination of mirror reflection and translation). Therefore, many different space groups can correspond to the same point group.
|