=================================================================================
The wave function of the focused probes in STEM and SEM is given by, [1,2]
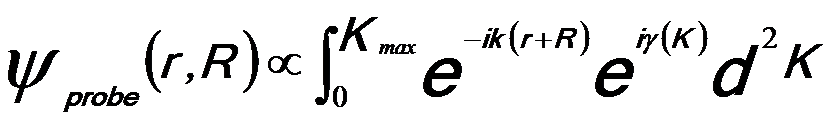 -------------------------[2579a] -------------------------[2579a]
where,
γ(K) -- The aberration function in radians (i.e., the phase difference between the aberrated wavefront and the ideal wavefront).
In Equation 2579a, the integration represents coherent sum over all contributions of waves passing through the probe-forming lens aperture. The first exponential term gives the relative path difference of different waves, while the second exponential term presents the overall aberration of the probe-forming electro-optical system.
For STEM, the beam-specimen interaction will modify the probe wave function at the exit side of the specimen comparing to that at the entrance side. Their relationship is given by,
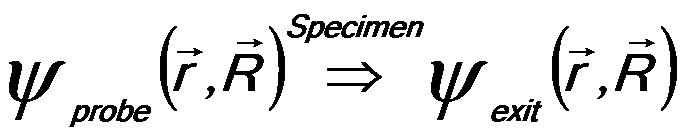 ----------------------- [2579b] ----------------------- [2579b]
The BF(bright field)-STEM intensity can be given by the summation of the directly transmitted and diffraction beams corresponding to the exit wave functions,
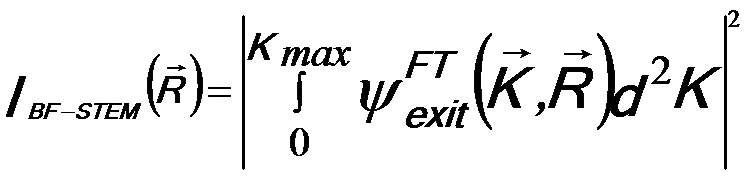 ---------------------[2579c] ---------------------[2579c]
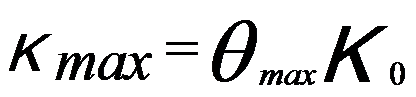 ----------------------- [2579d] ----------------------- [2579d]
where,
Kmax -- The maximum transverse wave-vector,
θmax -- The
maximum scattering angle collected by the BF-STEM detector.
The DF (dark field)-STEM intensity can also be given by the summation of the diffraction beams corresponding to the collected exit wave functions,
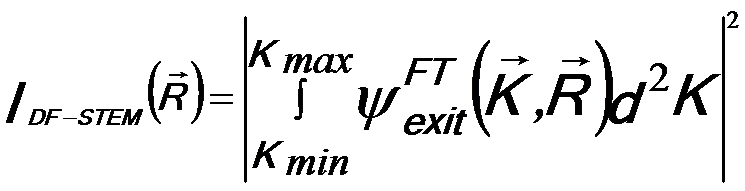 ---------------------[2579e] ---------------------[2579e]
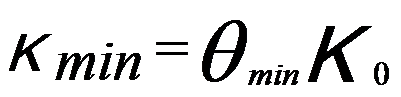 ----------------------- [2579f] ----------------------- [2579f]
where,
Kmin -- The minimum transverse wave-vector,
θmin -- The
minimum scattering angle collected by the DF-STEM detector.
The Fourier transform of the two-dimensional (2-D) exit wave is given by,
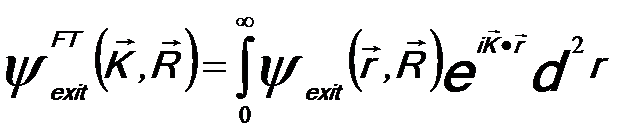 -------------------------[2579g] -------------------------[2579g]
In order to have relatively “pure” Z (atomic number) contrast, the typical values of the inner (θmin) and outer (θmax) angles for the annular DF detector used in HAADF-STEM are normally between 50 and 100 mrad for a 200-kV TEM. The key point is that the inner angle should be much larger than the typical scattering angle of coherent Bragg interaction.
In STEM analysis, the effect of the beam–specimen interaction in modifying the probe wave function into the sample exit wave function can be modeled using either the Bloch wave approach [3,4] or a multislice approach. [2,5]
[1] Hartel P. Ultramicroscopy 1996;63:93–114.
[2] Kirkland EJ, Loane RF, Silcox J. Ultramicroscopy 1987;23:77–96.
[3] Nellist P, Pennycook SJ. Ultramicroscopy 1999;78:111–24.
[4] Peng Y, Nellist PD, Pennycook SJ. J Electron Microsc 2004;53:257–66.
[5] Cowley JM, Moodie AF. Acta Crystallogr 1957;10:609–19.
|
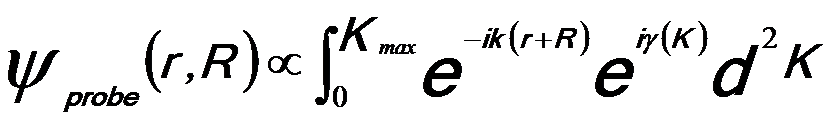 -------------------------[2579a]
-------------------------[2579a] 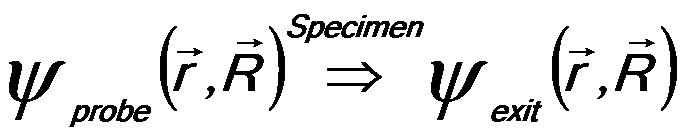 ----------------------- [2579b]
----------------------- [2579b] 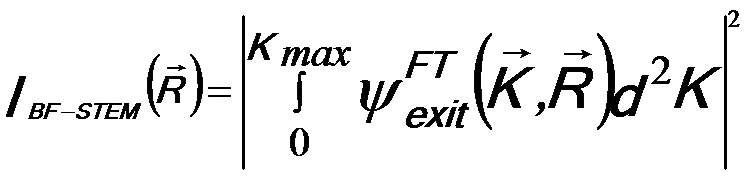 ---------------------[2579c]
---------------------[2579c] 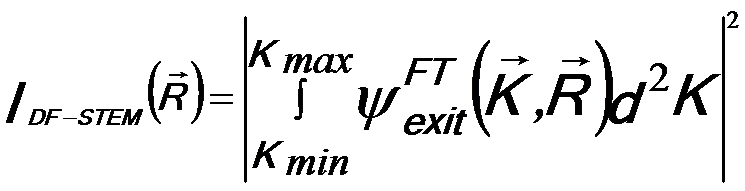 ---------------------[2579e]
---------------------[2579e] 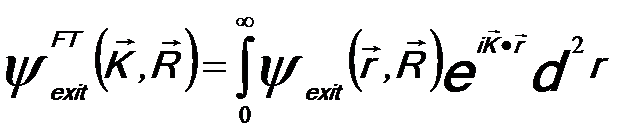 -------------------------[2579g]
-------------------------[2579g]