=================================================================================
Solid angle is derived from the Greek stereos, and the symbol for solid angle is Ω (Greek letter omega). The steradian (symbol: sr) is the SI unit (International System of Units) of solid angle. The solid angle can be defined in terms of an area on the surface of a sphere which is centred at the vertex of the angle. The solid angle is a dimensionless measure (like the radian) of how big an object appears to an observer (a point).
Solid angle can be simply given by,
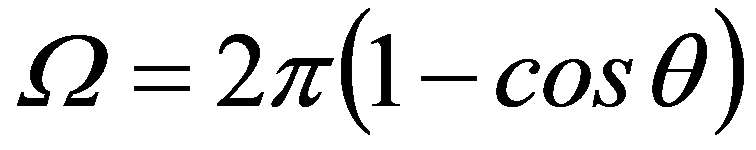 ---------------------------- [2671a] ---------------------------- [2671a]
Therefore, dΩ, as indicated in Figure 2671, is given by,
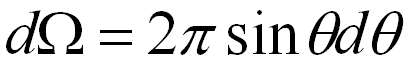 ---------------------------- [2671b] ---------------------------- [2671b]
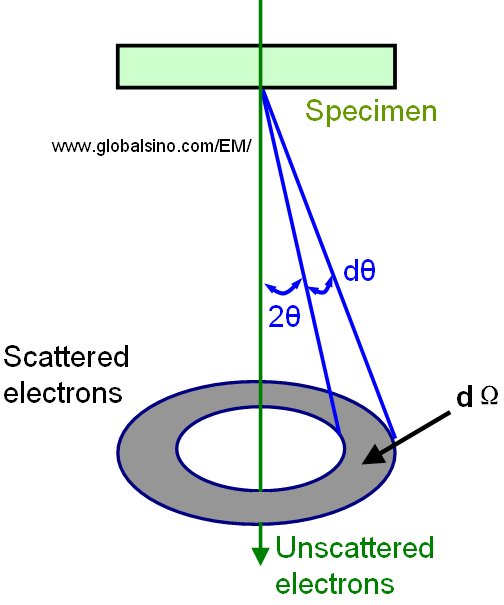
Figure 2671. Schematic illustration of scattering of an electron by a single atom.
Everyone knows what a 90° angle looks like, and even referring to it as π/2 radians is relatively easy to understand. However, it is a different matter altogether with solid angles since it must be imagined in three-dimensional (3-D) space without an obvious reference. For instance, one steradian is equal to (180/π)2 square degrees. Table 2671 lists some typical values of solid angles of some specific shapes.
Table 2671. Typical values of solid angles of specific shapes.
Shapes |
Solid angle measured at the centre (sr) |
Complete sphere |
4π |
Face of a cube |
2π/3 |
If the solid angle Ω in steradians is known, then the corresponding area of the surface of any sphere can be calculated by,
AS = R2·Ω ---------------------------- [2671c]
where,
R -- The radius of the sphere.
|
