=================================================================================
It was first introduced by Frank and van der Merwe [1] that a lattice-mismatched epitaxial alloy could be grown without misfit dislocations at the interface up to a critical thickness. Dislocations nucleate and propagate above this thickness. Two theories have been proposed to calculate the equilibrium critical thickness hc. The first theory [2 - 3] is based on the principle of energy minimization. The second theory [4] is known as the force balance theory. In 1974, Matthews and Blakeslee [5] proposed that the critical thickness would be reached when the lattice mismatch stress exerted a force that exceeded the line tension on a threading dislocation. For a general system the critical thickness hc can be given by,
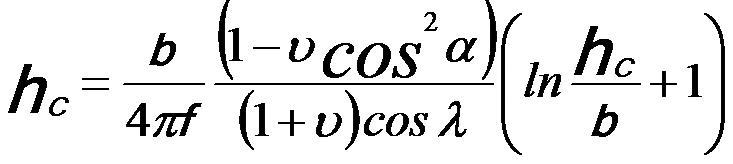 ---------------- [3381a] ---------------- [3381a]
where,
b -- Burgers vector
f -- The misfit strain
α -- The angle between the line of the misfit dislocation and its Burgers vector
λ -- The angle between the slip dislocation and the interfacial direction normal to the line of intersection of the slip plane and the interface
ν -- Poisson’s ratio
For instance, for the (001) SiGe/Si system in which the primary misfit dislocations are <110>{111}, critical thickness hc can be given by, [6]
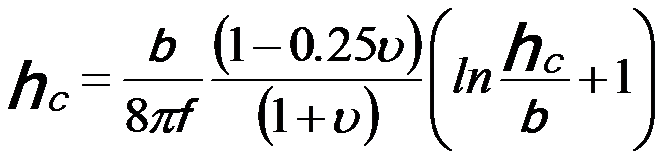 ---------------- [3381b] ---------------- [3381b]
Other factors can also determine the defect density in the strained epitaxial films. For instance, the defect density decreases as the single crystal area decreases.
The substrates for epitaxial growth of FePt films need to have similar atomic configuration to that of the FePt planes and thus result in small lattice mismatch. Table 3381 lists some FePt textures and the substrates required.
Table 3381. Some FePt textures and the substrates required.
| FePt planes |
Substrates |
Lattice mismatch |
| (001) <100> |
Cr (100) <110> |
5.8% |
| (001) <100> |
Ag (100) <001> |
7.1% |
| (001) <100> |
SrTiO3 (100) <001> |
2% |
| (001)<100> |
MgO (100) <001> |
8.5% |
[1] J. V. van der Merwe, Single Crystal Films, edited by M. H. Francombe and H. Sato (Pergamon, Oxford, 1964), p. 139.
[2] F. C. Frank and J. van der Merwe, One dimensional dislocations. II. Misfit monolayers and oriented overgrowth, Proc. Roy. Soc. (London), A 198, 216-25 (1949).
[3] C. A. B. Ball and J. H. van der Merwe, The growth of dislocation free layers, in Dislocations in Solids, F. R. N. Nabarro, Ed., (North Holland 1983), Chap. 27, pp. 122-41.
[4] J. W. Matthews, Coherent interfaces and misfit dislocations, in Epitaxial growth, Part B, Ed.: J. W. Matthews, (Academic Press, New York, 1975), pp 559 -609.
[5] J. W. Matthews and A. E. Blakeslee, J. Cryst. Growth 27, 118 (1974).
[6] S. R. Stiffler, J. Comfort, C. L. Stanis, D. L. Harame, E. de Frésart, and B. S. Meyerson, J. Appl. Phys. 70, 1416 (1991).
|
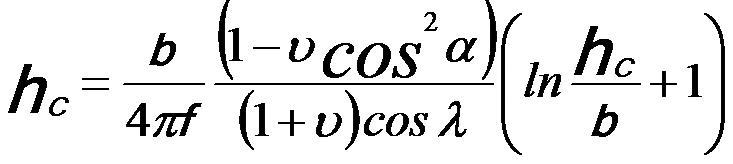 ---------------- [3381a]
---------------- [3381a] 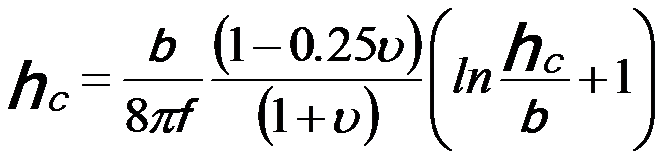 ---------------- [3381b]
---------------- [3381b]