=================================================================================
In general, angular distribution of scattered electrons is more conveniently
described in reciprocal space.
i) The inelastic scattering of electrons occurs at smaller angles than that for elastic scattering.
ii) Heavy atoms
that produce a large elastically scattered intensity outside the collection aperture of EELS measurements reduce the intensity of the EELS spectrum. Therefore, for a given experimental condition, counts in the ionization edges decrease as the probe is moved into
a region with strong elastic scattering.
iii) Phonon scattering produces large scattering
angles [6]. Phonon scattering cross-sections also increase
with the atomic number (roughly ∝ Z3/2 [7]).
iv) For thicker samples, elastic scattering causes the fraction of plural scattered electrons collected in the EELS entrance aperture to be different for different elements. [5]
Figure 3819a shows angular distributions of various scattered electrons as a function of scattering angle in EMs.
| Figure 3819a. (a) Elastic scattering of electrons with crystalline and amorphous specimens, (b) Phonon scattering, (c) Inner-shell ionization losses, and (d) Plasmon losses. |
Figure 3819b shows an example of angular-resolved electron scattering profiles in logarithmic scale. The reference spectrum (vacuum) in blue is dominated by unscattered electrons in the range −4 to 4 mrad. Due to the scattering of the incident electrons with a rhenium (Re) TEM specimen, the modified spectrum in red was formed.
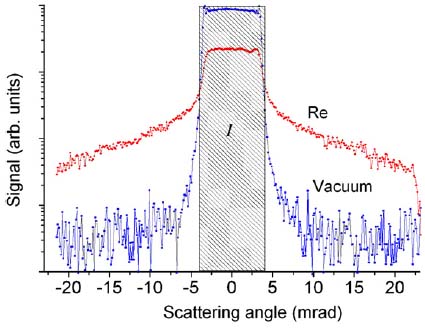
| Figure 3819b. An example of angular-resolved electron scattering profiles of electrons in vacuum and Re film in logarithmic scale.
[1] |
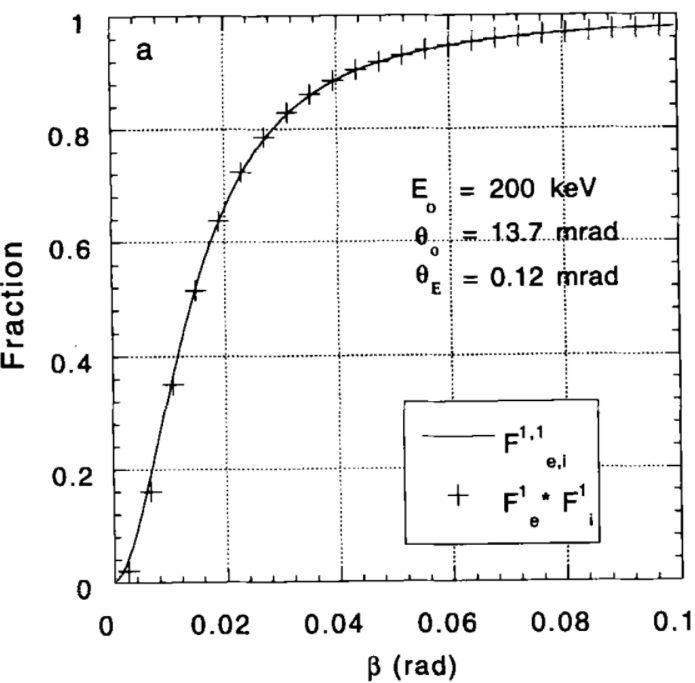
Figure 3819c shows the simulated fraction of 200-keV electrons entering a EELS collector aperture
of size β after mixed scattering in carbon (C). It can be seen that some incident electrons are scattered at very high angles or backscattered and thus they do not enter the EELS detector. The relative error in making the simulation approximation decreases with Z and increases with thickness. Broadening of the angular distribution exists if multiple elastic scattering is considered, comparing with single elastic scattering. In experiments [2], the elastic components were obtained
from the spectra using Gatan EL/P software. The
corresponding incident intensity for each low-loss spectrum was measured by moving the specimen out of the electron
beam.
 |
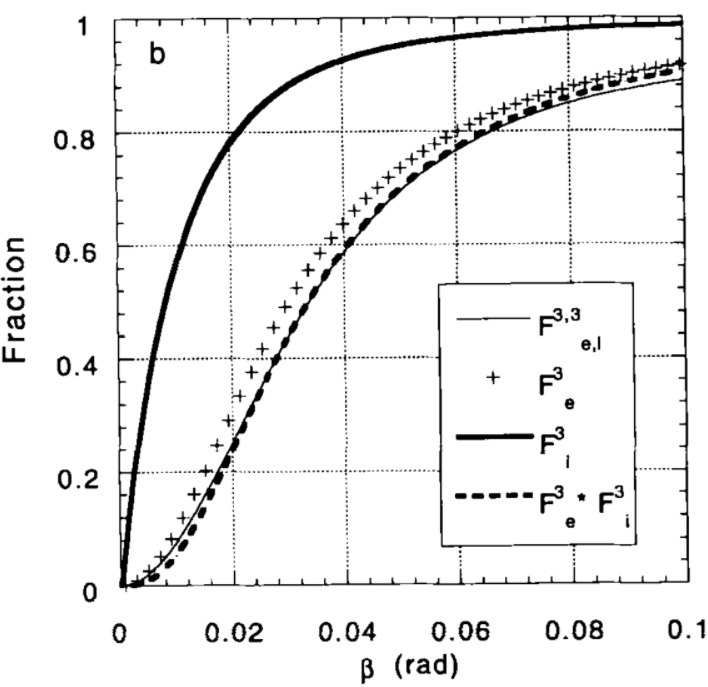 |
Figure 3819c. Fraction, simulated with Lenz model, of 200-keV electrons entering a EELS collector aperture
of size β after mixed scattering in carbon: (a) one elastic and one
plasmon. (b) three elastic and three plasmons.
[2] m represents elastic scattering and n for inelastic scattering in 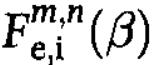 . . |
Increasing the TEM foil thickness broadens the angular distribution because the mean-free-path lengths for elastic scattering and plasmon losses are orders of magnitude smaller than those for K-shell ionization. [3] Theoretical studies suggest:
i) Calculations of the angular distribution of this “mixed” scattering based on the Lenz model with single-scattering distributions indicates [2]:
i.A) the m-fold elastic scattering
distribution approximates to a broadened single-scattering angular distribution with
θ0 replaced by (0.7+0.5m)θ0. Here, θ0 is the characteristic angle of elastic
scattering.
i.B) the corresponding aperture function can
be approximated by a simple product:
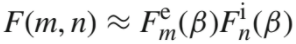 --------------------- [3819] --------------------- [3819]
here, the elastic and inelastic scattering
have very different angular widths.
ii) Calculations that include the contributions of elastic scattering [4] and convolutions of the energy and angular distributions of the scattering angle [5] demonstrate trends that are consistent with the experimental variation of the composition with thickness.
iii) Elastic scattering preferentially reduces the intensity of the
lower core-loss edge. Therefore, the relative ratios of the elements may be affected, unless very large collection apertures are use. [5]
iv) Decreas
of elastic scattering intensity in small angle ranges (less than several mrad) is expected due to plurality of scattering [2].
v) The minimum detectable number
of atoms in EELS measurements depends on the reduction of intensity by the
inelastic scattering of the other matrix elements that produce
a background [8].
[1] Konstantin Iakoubovskii and Kazutaka Mitsuishi, Elastic scattering of 200 keV electrons in elemental solids: experimental observation of atomic-number-dependent oscillatory behavior, J. Phys.: Condens. Matter 21 (2009) 155402.
[2] K. Wong and R. F. Egerton, Correction for the effects of elastic scattering in core-loss quantification, Journal of Microscopy, 178(3), (1995) pp. 198-207.
[3] Ludwig Reimer, Helmut Kohl, Transmission Electron Microscopy: Physics of Image Formation, 2008.
[4] Cheng, S.C. and Egerton, R.F. (1993). Micron 24, 251.
[5] Su, D.S., Wang, H.F. and Zeitler, E. (1995). Ultramicroscopy 59, 181.
[6] Z.L. Wang, J.M. Cowley, Ultramicroscopy 31 (1989) 437.
[7] R.F. Egerton, Electron Energy-Loss Spectroscopy in the Electron
Microscope, second ed., Plenum Press, New York, 1996.
[8] R.F. Egerton, R.D. Leapman, in: L. Reimer (Ed.), Energy-Filtering
Transmission Electron Microscopy, Springer-Verlag, Berlin, 1995, p.
269.
|