=================================================================================
The Radon transform is named after the Austrian mathematician Johann Karl August Radon [1]. The main application of the Radon transform is computed-axial-tomography (CAT scan), barcode scanners, line detection, electron microscopy of particles and macromolecular assemblies (e. g. viruses and protein complexes), and reflection seismology.
The Radon transform
projects a two-dimensional (2-D) intensity distribution into a two-dimensional (2-D)
parameter space. As shown in Figure 3866, applying the Radon transform on an image f (x,y) for a given set of angles can be considered as computing the projection of the image along the given angles. The source and sensor contrapment is rotated about the center of the object. For each angle α the rays from the source is accumulated at the sensor. This process is repeated for a given set of angels, e. g. from q ∈ [0; 180). Therefore, the Radon transform can be given by,
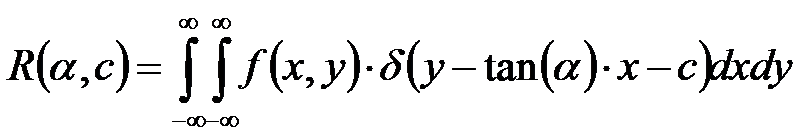 ---------------- [3866] ---------------- [3866]
where,
δ -- Dirac’s delta function
f(x,y) -- The intensity distribution in the two-dimensional
image
R -- The integral of f along the
curve which is given by the expression between the square
brackets of the δ function.
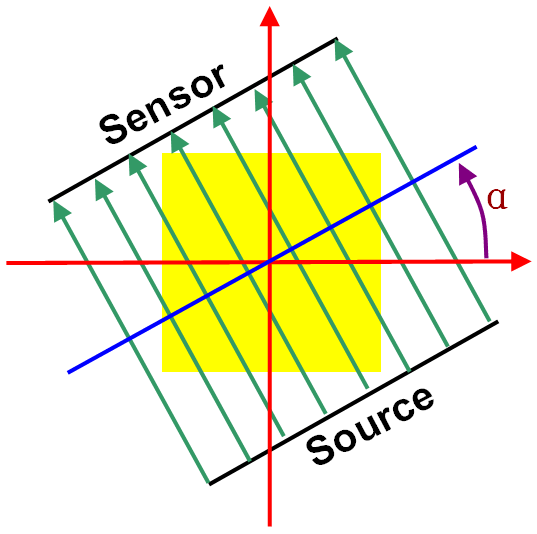
Figure 3866. Radon transform: The source and sensor contrapment is rotated about the center of the
object.
[1] Deans, S. R. (1981) Hough transform from the Radon transform. IEEE Trans. Pattern Anal. Machine Intell. 3, 185–188.
|
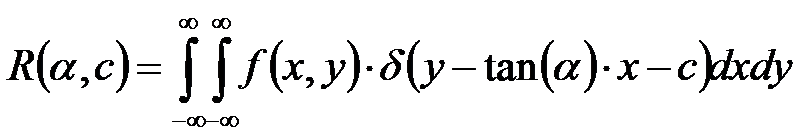 ---------------- [3866]
---------------- [3866] 