=================================================================================
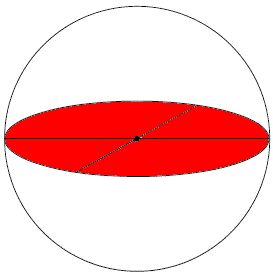
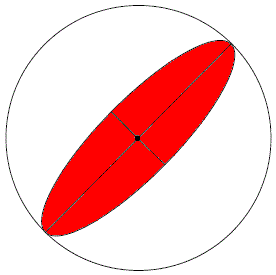
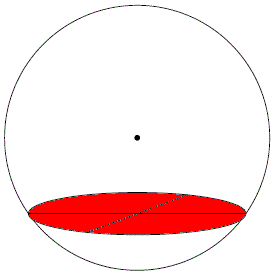
The stereographic projection is an analogous and powerful tool for working problems that involve relative orientations between two different crystals. Although these problems can be solved with rotation matrices, stereographic projections are quick and easy. By following the second step of the generation of stereographic projection, the Wulff Net is obtained from a calibrated reference sphere. The Wulff Net in Figure 4122a shows great circles all passing from the north pole to the south pole (longitude) and another around the equator (latitude), meaning that all the vertical arcs and the equator are great circles. As shown in Figure 4122b, great circles are the circles with diameters which equal to that of the sphere. In the Wulff Net, the lines of longitude are concave inwards and the lines of latitude are arcs. The great circles always pass through opposite ends of a diameter in the projection, meaning that a great circle is a line of intersection of planes that pass through the center of the sphere (like lines of longitude on Earth). Circles on the sphere which do not contain the center of the sphere are smaller, meaning a small circle is loci of all positions of a point on the surface of the sphere when rotated about an axis, e.g. the North pole. As shown in Figure 4122c, small circles are the circles with diameters which are less than that of the sphere.
The Wulff Net is useful for performing general rotations about the pole (plane normal) of the projection and is convenient for measuring angles between poles (plane normals) that lie along the same line of longitude. The highly symmetrical Polar Net contains less information than the Wulff net and is therefore less versatile than the Wulff net for performing crystallographic manipulations. Moreover, the Wulff net is convenient to rotate a crystal into any three-dimensional (3D) orientation.
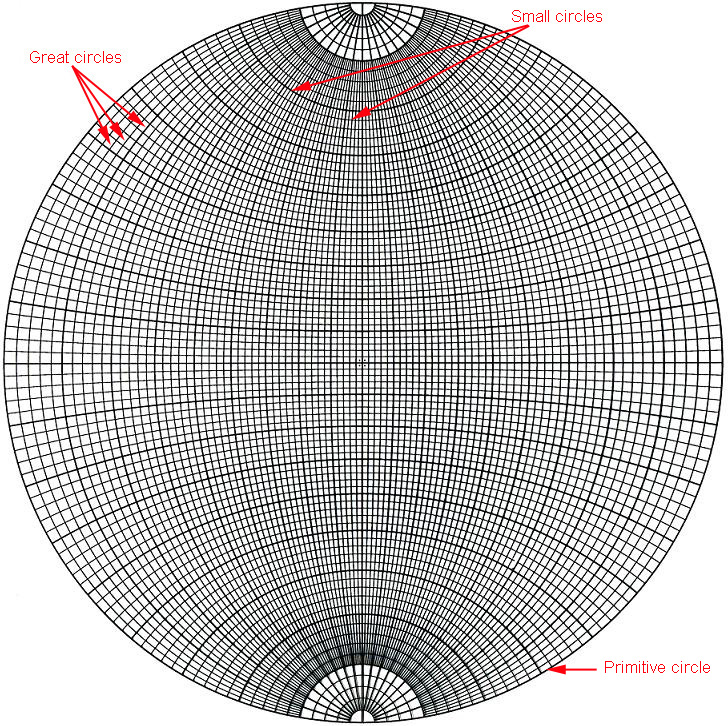
Figure 4122a. Wulff Net. Latitude measures north-south position and longitude measures east-west.
 |
 |
(a) |
(b) |
Figure 4122b. Example of great circles in red.
 |
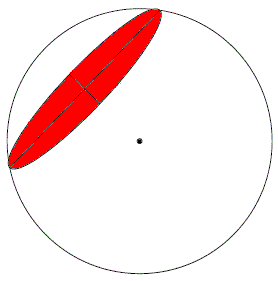 |
(a) |
(b) |
Figure 4122c. Example of small circles in red.
| Functions of Wulff Net |
To measure the angle between two directions
To find the pole of great circle
To find the great circle corresponding to a pole
To use great circles to measure angles
To find the angle between two planes
To rotate projection around an axis lying in the plane of projection. |
Different manipulations can be performed with the Wulff Net. Firstly, the Wulff Net can be used to rotate a crystal into any three-dimensional (3-D) orientations, which probably requires several independent operations. For instance, it can be a series of i) A simple rotation about the north pole of stereographic projection, and then ii) A simple rotation about the north pole of the Wulff net. Secondly, the Wulff Net can be used to perform mirror reflections about a plane of a crystal.
When we use the Wulff net as a tool to rotate a crystal in three-dimension (3-D), these rotations can include various independent operations such as:
i) Rotation about the north pole of the stereographic projection which is the center of the projection.
ii) Rotation about the north pole of the Wulff net, including movement of poles along the lines of latitude.
iii) Use the Wulff net to perform mirror reflections about a plane of a crystal.
|
