=================================================================================
Spherical aberration has played a central role in electron microscopy. In conventional TEM system, the existence of spherical aberration requires the utility of very small apertures to maximize the spatial resolution, while the resolution will also be limited by diffraction (see Airy disc) if the apertures are too small. For five decades, it had been the engineering constraint.
For optical microscope, most photographic lenses are composed of elements with spherical surfaces. Such elements are relatively easy to manufacture, but their shape is not ideal for the formation of a sharp image. Spherical aberration (SA) is an image imperfection that is due to the spherical lens shape. The spherical aberration also exists in electron microscopes (EMs). Note that a shorter focal length of objective lens provides smaller spherical aberration and higher spatial resolution, while a longer focal length gives higher image contrast. In reality, in traditional TEM the spherical aberration coefficient of a round lens is always positive and on the order of its focal length. Spherical aberration causes the incident electrons with different angles to the optical axis to be focused at different distances.
Spherical aberration as one type of geometric aberrations in EMs was considered by Scherzer. For instance, the spherical aberrations of the objective lenses of EMs affect strongly the image formation of the electron microscope.
Spherical aberration is the only form of monochromatic axial wavefront aberration produced by rotationally symmetrical surfaces centered and orthogonal in regard to the optical axis. The spherical attribute is due to this aberration being inherent to the basic optical surface - spherical - for object at infinity. Spherical aberration affects the entire image field, which makes its correction first priority. As shown in Figure 4579 (a), the parallel light or electrons passing through the periphery of the lens are focused more strongly than those passing through the centre and the circle of the least confusion (the best focus point) is located within the range of longitudinal spherical aberration. On the other hand, in Figure 4579 (b) the electrons leaving the point P of the object are refocused at P' instead of P''. Consequently, in the image plane the point is imaged as a disk with radius (Δrs) given by,
 ---------------------------- [4579a] ---------------------------- [4579a]
where,
β -- The lens aperture.
Therefore, the point resolution deteriorates with increasing β.
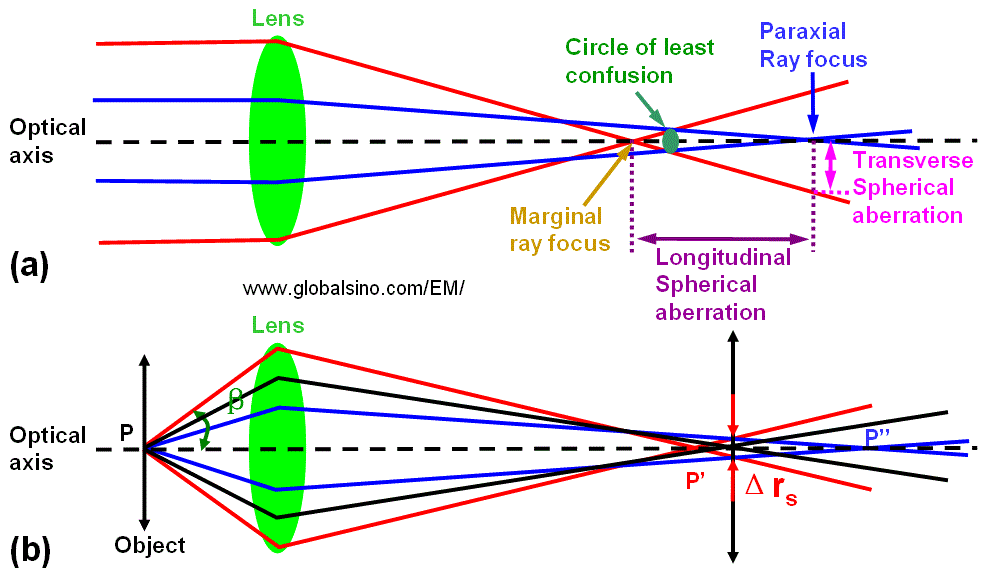
Figure 4579.
Schematic diagram of
spherical aberration (SA): (a) Focusing
an initially parallel beam, and (b) Focusing electrons from an object.
Practically, the large, and positive third-order spherical aberration is combined with a optimized defocus setting (namely, sample height Z = C1,0) to form the Scherzer λ/4 phase plate,
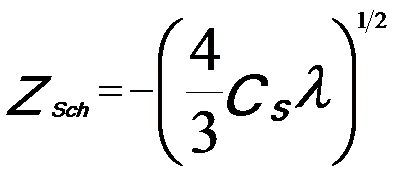 ---------------------------- [4579b] ---------------------------- [4579b]
So that the point resolution is,
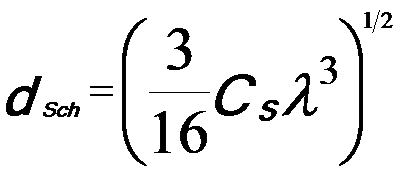 ---------------------------- [4579c] ---------------------------- [4579c]
In this case, the object information up to a spatial frequency 1/dSch is transferred with the same sign of the aberration function, yielding dark-atom contrast for a TEM specimen that can satisfy weak phase object approximation (WPOA) condition.
The physical origin for the formation of spherical aberration in the actual magnetic lenses is due to the fact that the electromagnetic potentials satisfy Laplace’s equation in the domain of the electron trajectories. Therefore, the spatial distribution of the index of refraction of electron lenses cannot be formed arbitrarily. Since the potential adopts an extremum at the lenses’ boundaries, the outer (marginal) zones of rotationally symmetric electron lenses always focus the rays more strongly than the inner (paraxial) zones, causing the spherical aberration.
Table 4579 lists the aberration coefficient nomenclature, their order (of both the ray deviation (N) and the wavefront), and radial (azimuthal) symmetry. This table also compares both commonly used notations [1, 2]. The spherical aberration coefficients are highlighted in green and are usually the most significant among all the aberrations. The third- and fifth-order spherical aberration coefficients and defocus (first order spherical aberration) are present in a perfect, round electromagnetic lens, while all other higher-order coherent aberration coefficients are caused by lens imperfections. Those higher-order aberration coefficients can become important at high spatial resolutions because of the increasing order of their spatial frequency dependence.
Table 4579. Aberration Coefficient Nomenclature. The aberration coefficients have two
main types of notations, namely Krivanek notation, and Typke and Dierksen notation.
| Krivanek notation |
Typke and Dierksen notation |
Radial Order |
Azimuthal Symmetry |
Nomenclature |
| Ray |
Wave (k) |
| C0,1 |
A0 |
0 |
1 |
1 |
Image Shift |
| C1,2 |
A1 |
1 |
2 |
2 |
Two-fold axial astigmatism (or axial astigmatism of the 1st order) |
| C1,0 |
C1 |
1 |
2 |
0, ∞ |
Defocus (overfocus positive, or spherical aberration of the 1st order; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Δf) |
| C2,3 |
A2 |
2 |
3 |
3 |
Three-fold axial astigmatism (or axial astigmatism of the 2nd order)
|
| C2,1 |
B2 |
2 |
3 |
1 |
Axial coma |
| C3,4 |
A3 |
|
4 |
4 |
Four-fold axial astigmatism or axial astigmatism of the 3rd order Cs |
| C3,2 |
B3 |
|
4 |
2 |
Twofold astigmatism of Cs (or Third order twofold astigmatism, or Axial star aberration of the 3rd order) |
| C3,0 |
C3 |
|
4 |
0, ∞ |
Third-order spherical aberration (always positive for round lenses [3]; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Cs ) |
| C4,5 |
A4 |
|
5 |
5 |
Five-fold axial astigmatism or axial astigmatism of the 4th order |
| C4,1 |
B4 |
|
5 |
1 |
Fourth-order axial coma |
| C4,3 |
D4 |
4 |
5 |
3 |
Fourth order threefold astigmatism (or Three lobe aberration) |
| C5,6 |
A5 |
|
6 |
6 |
Six-fold axial astigmatism or sixfold axial astigmatism of the 5th order |
| C5,4 |
R5 |
5 |
6 |
4 |
Fourfold astigmatism of C5 (or Fifth order rosette aberration) |
| C5,2 |
S5 |
5 |
6 |
2 |
Twofold astigmatism of C5 (or Fifth-order axial star aberration) |
| C5,0 |
C5 |
|
6 |
0, ∞ |
Fifth-order spherical aberration |
| |
D5 |
|
|
|
Four lobe aberration of the 5th
order |
It is interesting to mention that ideally the aplanatic lenses, which can in some cases be condenser or objective lenses, are free of spherical aberration and off-axial coma simultaneously. Because the spherical aberration in general is unavoidable for rotationally symmetric electron lenses in EMs (electron microscopes), it can never be aplanatic. However, each electron lens has a coma-free point that locates on the optic axis within the field of the lens. No coma is introduced into the images by any off-axial pencil of the rays whose central ray intersects the coma-free point. In aberration-corrected TEMs, in order to eliminate the off-axial coma, the coma-free point of the lens next to the corrector must match the corresponding point of the corrector field.
Note that the intensities of the electron diffraction (ED) pattern from a crystalline specimen are independent of defocus and the spherical aberration of the electron-optical system.
If the spherical aberration (Cs) is zero in a Cs-corrected microscope, positive phase contrast of a weak-phase object can still be obtained by the defocus,
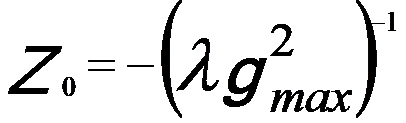 ----------------------------------- [4579d] ----------------------------------- [4579d]
This condition presents a pass band up to the information limit (gmax) at the contrast delocalization of R0 = 1/gmax.
Due to the positive spherical aberration in traditional TEMs, the only way to produce phase contrast from a thin object is to use an underfocus setting. The resulting aberration function from underfocus is negative and the phase change is positive. The positive phase contrast from a weak phase object is thus dark with respect to the background (mean intensity).
[1] Krivanek, O. L., Dellby, N., and Lupini, A. R. (1999). Towards sub-Å electron beams.
Ultramicroscopy 78, 1.
[2] Typke, D., and Dierksen, K. (1995). Determination of image aberrations in high-resolution
electron microscopy using diffractogram and cross correlation methods. Optik 99, 155.
[3] O. Scherzer, J. Appl. Phys. 20 (1949) 20.
|