=================================================================================
We know that the sizes of the BF- and DF-detectors are fixed. Therefore, in principle, it is easy to understand that the transmitted electrons or different diffracted beams can be collected by moving the detectors (screen) down or up, as shown in Figure 4938a, which corresponds to the change of the camera length.
However, a couple of reasons make the detector movement impossible, for instance:
i) It is not convenient to mechanically move the detectors up and down in a vacuum condition.
ii) The proper camera lengths for different applications can be from cm to 30 m. The vacuum column does not such a wide room to move the detectors.
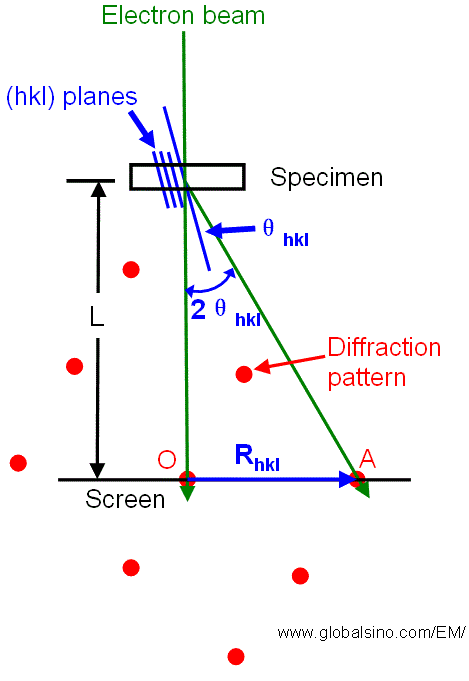
| Figure 4938a. Relationship between the reciprocal lattice spacing Rhkl and the camera length L for diffraction in a TEM. |
However, instead of moving the detectors up and down to select and record the intensities of the transmitted and/or different diffracted beams, we can conveniently change the lens currents to zoom in (magnify) or zoom out (demagnify) the diffraction pattern on the detectors. This zoom-in and zoom-out process are then converted to the correpsonding camera lengths on the commercial microscopes. Therefore, the collection angles of the detector can be varied simply by changing the effective camera length.
In TEM and in normal STEM systems with postspecimen
lenses the situation is more complicated because the postspecimen lenses have the property of changing beam angles. In TEM systems, one has further to distinguish between image mode (image on fluorescent screen) and diffraction mode (diffraction pattern on fluorescent screen). Table 4938 shows how to determine α and β by the apertures in the STEM and TEM. If a small objective aperture is inserted, it may limit β as indicated in Table 4938; the effective value of β at the back
focal plane of the projector lens is β/M where M is the
magnification of the image in the back focal plane of the
projector lens.
Table 4938. Aperture factors affecting α and β.
| |
Dedicated STEM |
Image Mode in TEM |
Diffraction Mode in TEM |
| α |
Objective aperture |
Condenser aperture |
Condenser aperture |
| β |
Condenser aperture |
Objective aperture |
The smaller of selected area and objective aperture |
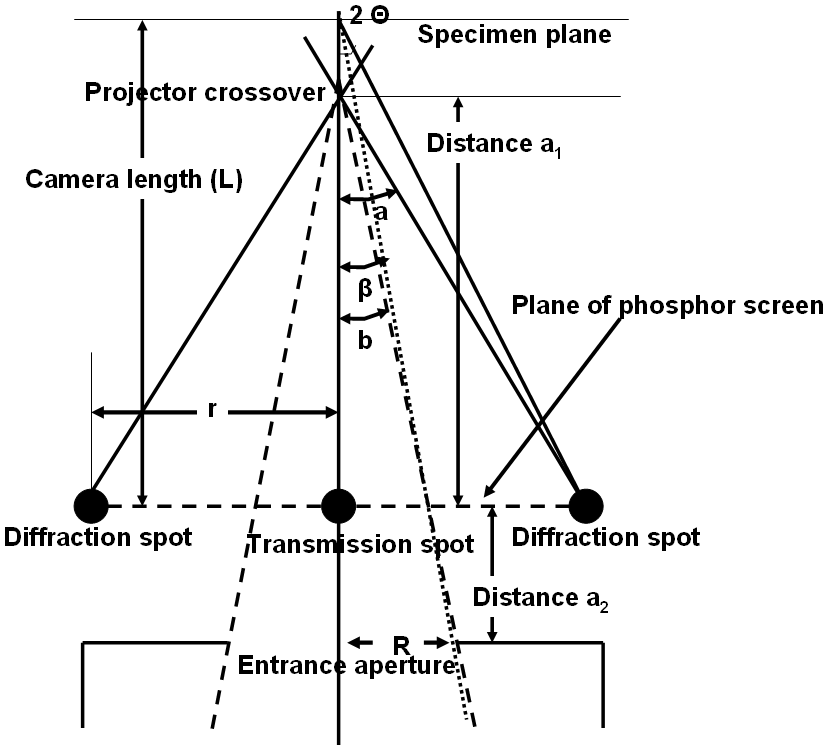
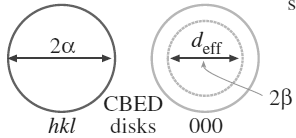
Figure 4938b. α and β calculation by considering entrance aperture of GIF camera.
In the diffraction mode, β is determined by the camera length. If there is no lenses after the TEM specimen, β would be simply be β = r/(L+a2).
As shown in Figure 4938b, in STEM and TEM diffraction modes, the diffraction pattern is similar to convergent beam electron diffraction (CBED) in TEM mode because of using the focused electron beam. On the other hand, with a projector crossover the diffraction patern looks as if it were being projected from a distance of L (camera length), but it is actually coming from the crossover. Angle b is fixed for any PEELS and EELS entrance aperture, β depends on the ratio of b/a. β = (b/a) 2Θ, here Θ is from Bragg equation λ = 2d sinΘ, and λ and d are wavelength of electron beam and d-spacing. Doing all the algebra and goemetry will give,
β = (R*a1)/(D*L) = Reff/L---------------------------------------------- (4938)
where R - radius of entrance aperture
a1 - distance between projector crossover and phosphor screen (recording plane)
D - distance between projector crossover and entrance aperture (=a1 + a2)
L - camera length
Reff - effective entrance aperture radius
D is typically 600 mm for Gatan PEELS/EELS systems but a1
varies depending on the TEM system. Assuming a1 is 500 mm and L is 800 mm
then for an aperture (R) of 2.5 mm in radius, β is ~ 2.6 mrads.
For α > β, the geometrically given collection angle
should be replaced by an effective angle [1].
The schematics in Figure 4938c shows the electron optical column in a modern analytical electron microscope operated in STEM mode, indicating the projector lens controlling detector collection angle.
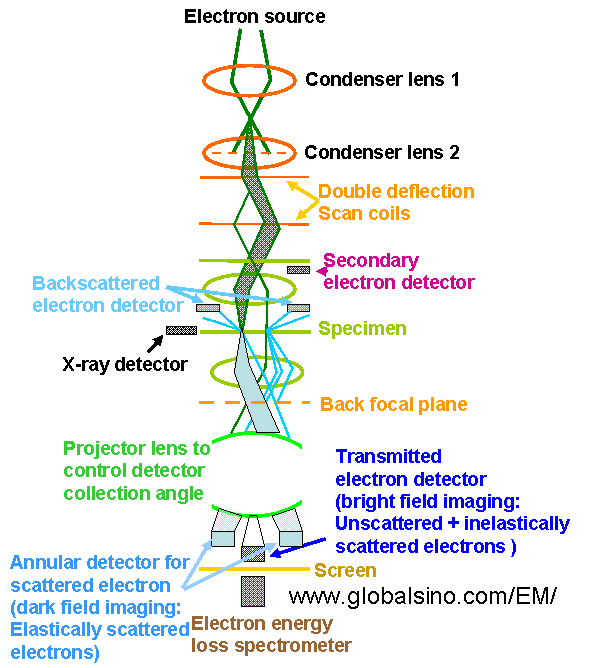
Figure 4938c. Schematics of the electron optical column in a modern
analytical electron microscope operated in STEM mode.
[1] Egerton RF. 1996. Electron Energy-Loss
Spectroscopy in the Electron Microscope.
New York/London: Plenum. p 485.
|