=================================================================================
Fourier transform plays an important role in TEM imaging and analysis, e.g. for HRTEM. There are a number of different conventions when Fourier transform is used. The most common convention in crystallography is given by the Fourier transform function f(r),
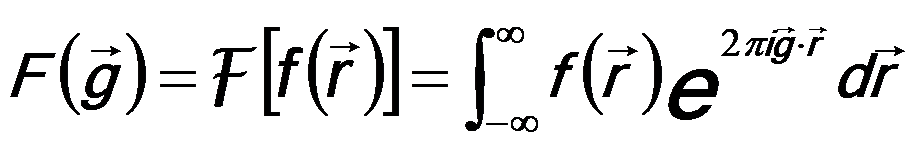 ------------------- [4974a] ------------------- [4974a]
where,
r -- A three-dimensional position vector in direct space,
g -- A three-dimensional position vector in reciprocal, space, or
Fourier transform.
The inverse Fourier transform is given by,
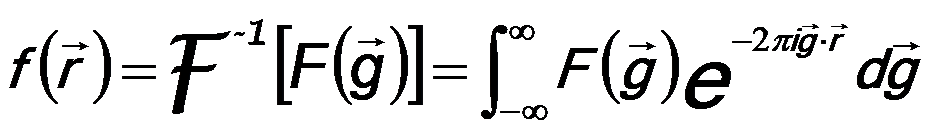 ------------------- [4974b] ------------------- [4974b]
When Fourier transform is performed on a set of sampled data, discrete Fourier transform (DFT) must be used instead of continuous Fourier transform (CFT) above. Note that the most common implementation of DFT on computers is fast Fourier transform (FFT) algorithm.
Simply speaking, Fourier transform is a limiting case of Fourier series. The structure factor F(u) is proportional to the Fourier components Iim(u) of the HREM image. For a weak-phase-object, the Fourier transform of the HREM image Iim(u) can be given by [1],
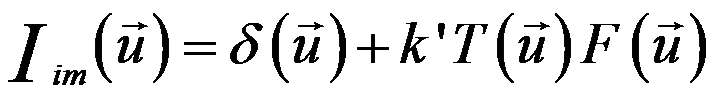 ------------------- [4974c] ------------------- [4974c]
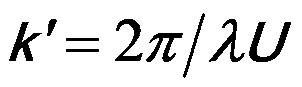 ---------------------- [4974d] ---------------------- [4974d]
Or,
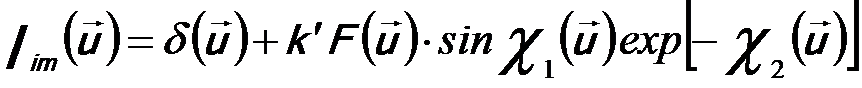 -------------- [4974e] -------------- [4974e]
where,
k’ -- A constant
T(u) -- The contrast transfer function (CTF) (= sinχ1(u) exp [-χ2(u)] )
F(u) -- Structure factor of electron diffraction (ED), which is the Fourier transform of the potential distribution φ(r) of the object
λ -- The electron wavelength
U -- The accelerating voltage of incident electrons
u -- The reciprocal-lattice vector within the resolution limit
Equation 4974c states that the Fourier component Iim(u) is proportional to the structure factor F(u) multiplied by the contrast transfer function (CTF).
If f(r) is a real-space function and g(u) is its Fourier transform, then
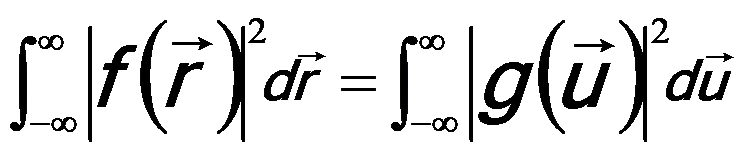 -------------- [4974f] -------------- [4974f]
Based on the theory of contrast transfer function (CTF), The dark rings of Fourier transform of HRTEM images locate at sin χ1(u) ≈ 0, so that,
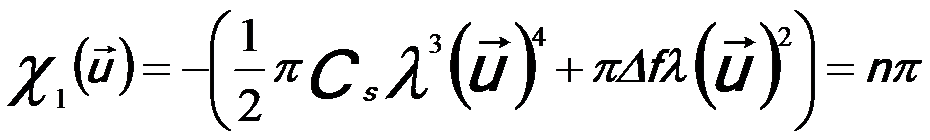 ------------------- [4974g] ------------------- [4974g]
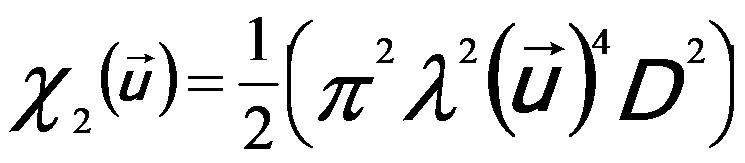 ------------------- [4974h] ------------------- [4974h]
Here, n = 0, ±1, ±2, .. are integers. And,
Δf -- The defocus value
Cs -- The spherical aberration
coefficient
D -- The standard deviation of the Gaussian distribution of defocus due to the chromatic aberration [2]
The values of Δf, Cs, and D can be obtained by TEM image deconvolution. Of these three factors, Cs and D can be determined experimentally. With the estimated values of Cs and D, a set of structure factor of ED F(h) can be calculated from equation of Fourier transform (Iim(u)) for a given value of Δf.
[1] X. D. Zou. Crystal Structure determination by crystallographic image processing. in
“Electron Crystallography”, eds. D. L. Dorset, S. Hovmöller, X. D. Zou, Nato ASI Series C,
Kluwer Academic Publishers, Dordrecht, 1997, pp163-181.
[2] Fijes PL. 1977. Approximations for the calculation of high-resolution
electron-microscopy images of thin films. Acta Cryst A33:109–113.
|
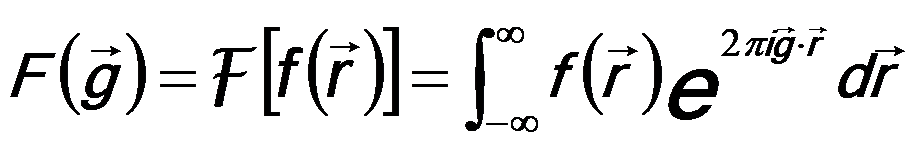 ------------------- [4974a]
------------------- [4974a] 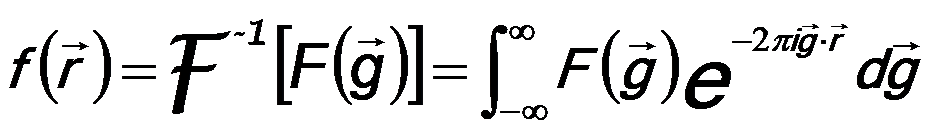 ------------------- [4974b]
------------------- [4974b] 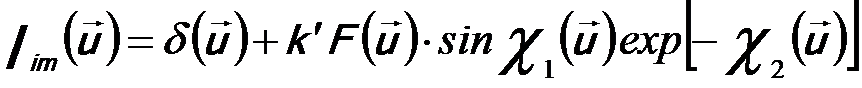 -------------- [4974e]
-------------- [4974e] 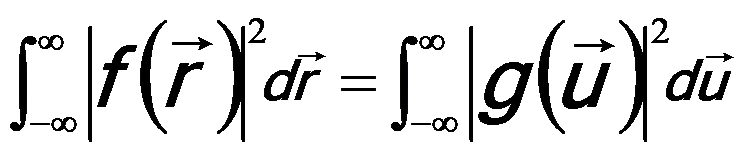 -------------- [4974f]
-------------- [4974f] 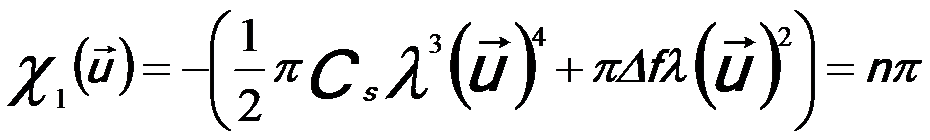 ------------------- [4974g]
------------------- [4974g] 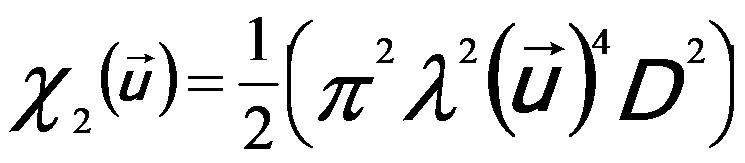 ------------------- [4974h]
------------------- [4974h]