Areal Density, N, is the number of atoms per unit area of the TEM sample through the electron beam. It has been proposed to extract the Areal Density in different ways:
i) Based on Partial Cross-Section theory.
In this way, by assuming that the probability of combined plasmon–core-loss multiple excitations included within the core-loss energy window Δ is the same as the fraction that falls within the low-loss integration window of equal width Δ, then the Areal Density, N, can be obtained by, [1,2]
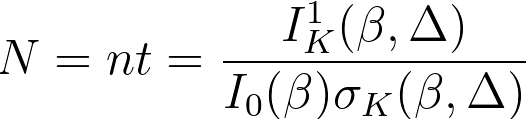 ---------------------------------------- [950a] ---------------------------------------- [950a]
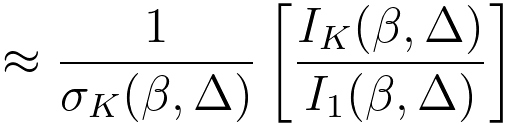 ---------------------------------------- [950b] ---------------------------------------- [950b]
where,
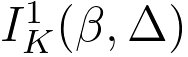 -- the corresponding SSD (single-scatter distribution) intensity. However, in practice, the quantity of the SSD is often unavailable. -- the corresponding SSD (single-scatter distribution) intensity. However, in practice, the quantity of the SSD is often unavailable.
I0 -- the zero-loss intensity,
n -- the number of atoms per unit volume of the sample, or so-called the concentration of the element,
t -- the sample thickness,
σK(β,Δ) -- the partial cross-section of K-shell, EK after background removal. This can be determined by theoretical calculation (e.g. with hydrogenic or Hartree–Slater models) or experimental measurement.
IK(β,Δ) -- the electron signal recorded, by an EELS spectrometer system with entrance semi-angle β, from K-shell losses between EK and EK + Δ (from the energy window Δ),
I1(β,Δ) -- the corresponding low-loss intensity, namely the plamon signal recorded under the same conditions (from the same energy window with an energy loss range of 0 and Δ, which includes the entire zero-loss peak), which corrects the effects of plural scattering.
Note that, to evaluate the concentration using Equation 950b, the absolute thickness t has to be determined.
ii) Based on zero-loss peak. [2]
In this method, the core-loss
signal can be used to quantify elemental concentrations, after removal of the background contribution and
possible deconvolution of plural scattering,
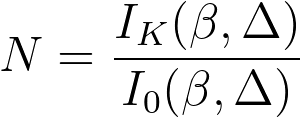 --------------------------------------------------------------------- [950c] --------------------------------------------------------------------- [950c]
where,
I0(β,Δ) -- the zero-loss integral intensity.
This method is based on the approximation that the probability of electrons, entering the angle-limiting aperture is the same for both elastic and inelastic scattering processes. However, this assumption is inaccurate in most cases since their scattering probabilities dependence on many factors such as TEM sample thickness and atomic numbers of the materials.
[1] R. F. Egerton, K-shell ionization cross-sections for use in microanalysis, 4(2), (1979) 169-179.
[2] P.J. Thomas and P.A. Midgley, An introduction to energy-filtered transmission electron microscopy, Topics in Catalysis, 21 (4), (2002), 109.
|