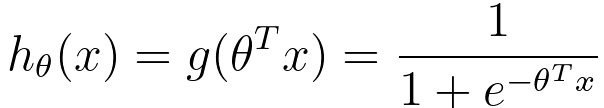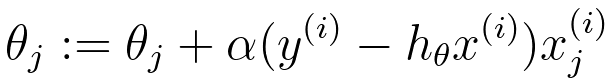=================================================================================

As discussed in support-vector machines (SVM), we have,

          --------------------------------- [3869]

Equation 3869 is a basic representation of a single-layer neural network, also known as a perceptron or logistic regression model, depending on the choice of the activation function g.

Table. 3869. Perceptron algorithm versus logistic regression.

	Perceptron algorithm	Logistic regression
Nature	Perceptron is a simpler model, providing binary classification based on a hard threshold.	Logistic regression provides probabilistic outputs and can be used for more complex tasks like ranking.
Model Representation	The Perceptron is a simple linear binary classification model. It computes a weighted sum of input features and applies a step function to make a binary decision.	Logistic regression is a probabilistic binary classification model. It models the probability of an example belonging to the positive class.
Learning Algorithm	Perceptron learning algorithm updates the weights based on misclassified examples, which can lead to convergence issues if data is not linearly separable. It can be expressed as:	Logistic regression uses the maximum likelihood estimation (MLE) to estimate the model parameters (weights and bias). The cost function for logistic regression is the log-likelihood, and gradient descent or other optimization methods are used to minimize it. Cost Function:
Output Range	Perceptron provides binary output (0 or 1):	Logistic regression provides a probability score between 0 and 1, making it more interpretable:
Decision Boundary	Perceptron finds a linear decision boundary that separates the two classes. Perceptron enforces a strict linear decision boundary, and is always linear.	The decision boundary of logistic regression is a probabilistic threshold (usually 0.5). It's not necessarily linear and can be non-linear depending on the data and feature transformations. Logistic regression can model non-linear decision boundaries. It can model linear or non-linear decision boundaries, depending on the data and feature space.
Hypothesis function
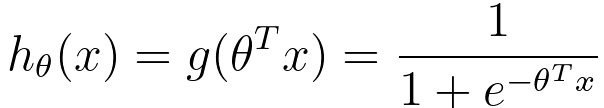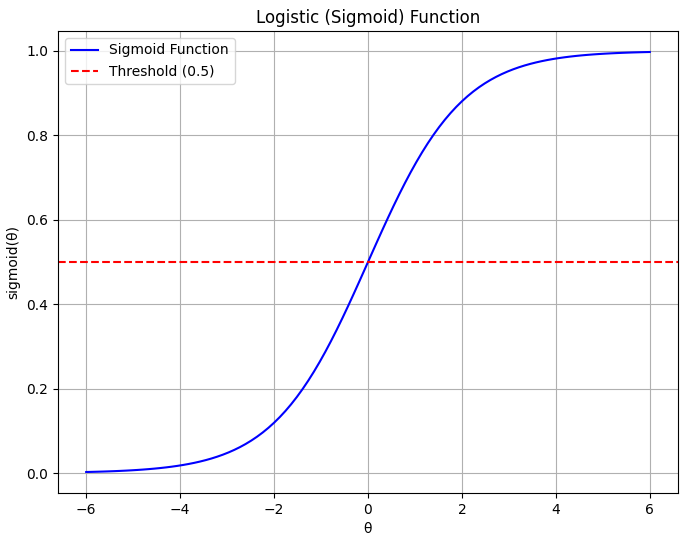
	The Perceptron uses a linear combination of input features followed by a step function (Heaviside function) to make predictions. Hypothesis Function: h(x) = sign(w•x + b) h(x): Predicted class (either +1 or -1) w: Weight vector x: Input feature vector b: Bias term	Logistic regression uses the logistic (sigmoid) function to model the probability of the positive class. Hypothesis Function: h(x): Predicted probability of the positive class w: Weight vector x: Input feature vector b: Bias term
θ update
Parameter Optimization	Uses the Perceptron learning rule to update weights based on misclassified examples.	Uses gradient descent or other optimization algorithms to minimize a cost function (e.g., cross-entropy loss).
Loss Function	No explicit loss function, but it updates weights to minimize misclassification.	Typically uses the cross-entropy (log loss) as the loss function.
Convergence	Guaranteed to converge if the data is linearly separable; otherwise, it may not converge.	Converges for most datasets, even if they are not linearly separable.
Probabilistic Interpretation	Lacks a probabilistic interpretation.	Provides a probabilistic interpretation of the class membership probability.
Applicability	Perceptron is generally used for simple linear classification tasks.	Logistic regression is widely used in various fields, including medical diagnosis, natural language processing, and more.
Application	Historically used for binary classification tasks, but less common in practice due to its simplicity.	Widely used for binary classification, and it can also be extended to multi-class classification and used for probability estimation.

============================================