Logistic Regression - Python for Integrated Circuits - - An Online Book - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Python for Integrated Circuits http://www.globalsino.com/ICs/ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Chapter/Index: Introduction | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Appendix | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
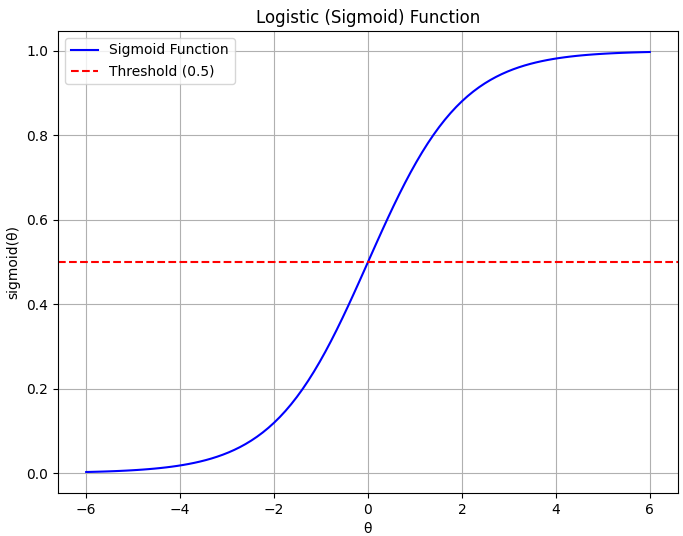
================================================================================= Logistic regression is a statistical method used for binary classification, which means it is employed to predict the probability of an observation belonging to one of two possible classes or categories. It is a type of regression analysis used for predicting a binary outcome (1 / 0, Yes / No, True / False) based on one or more predictor variables. It is a widely used machine learning algorithm in various fields, including medicine, finance, and marketing, due to its simplicity and interpretability. The key idea behind logistic regression is to model the relationship between a set of independent variables (features) and a binary dependent variable (target) by using the logistic function (also known as the sigmoid function). The logistic function maps any input value to a value between 0 and 1, namely hθ(x) ∈ [0,1], which can be interpreted as the probability of the observation belonging to one of the two classes. Then, we have hypothesis fuction given by: where:
g(z) is given by, Overall, we have, E[y|x;θ] can be the mean of a Bernoulli distribution in some case of applications. In general, the formula for the logistic function can be given by, where,
The plot in Figure 3876a shows a logistic regression decision boundary with two features.
(a)
(b)
In logistic regression, we have: p(y=1|x; θ) = hθ(x) ---------------------- [3876e] p(y=0|x; θ) = 1 - hθ(x) ---------------------- [3876f] By combining Equations 3876d and 3876e, we can get, The expression in Equation 3876d is a representation of the probability that a binary outcome variable y is equal to 1 (often considered the "positive" or "success" class) given a set of input features x and the model parameters θ. The target variable y equals 1 (i.e., Pr(y=1)). This is the hypothesis function in logistic regression. It is also referred to as the logistic function or sigmoid function. The sigmoid function takes the linear combination of the input features x and model parameters θ and "squashes" it into a range between 0 and 1. The formula for the sigmoid function in Equation 3876a. In Equation 3876e, the probability that y is equal to 0 (the negative class) is given by 1 minus the probability that y is equal to 1. This is because there are only two possible outcomes in binary logistic regression, and the probabilities of these two outcomes must sum to 1. We know likelihood function can be given by (see page3997), where,
In logistic regression, we aim to maximize the likelihood (Equation 3876i) of the observed data, which is represented as the product of the conditional probabilities of the actual outcomes given the input data and model parameters. Combining Equations 3876f and 3876h, then we can get, Then, we have, The goal of the calculation above is that we need to maximize ℒ(θ) by choosing a proper θ. The cross-entropy loss function can be given by, where,:
To find the optimal parameters θ, we typically maximize the log-likelihood, which is the natural logarithm of the likelihood: With the consideration of regularization consideration, we can have, This is the regularized log-likelihood function used in regularized logistic regression (also known as L2 regularization or Ridge regularization). In this case, we have an additional term, - λ||θ||2, which is a penalty term on the magnitude of the model parameters θ. This term is used to prevent overfitting by discouraging overly complex models with large parameter values. The λ (lambda) parameter is a hyperparameter that controls the strength of the regularization; larger values of λ lead to stronger regularization. The difference between Equations 3876kb and 3876kc lies in the regularization term "- λ||θ||^2" in the second expression. The regularization term encourages the model to have smaller parameter values, which can improve the generalization of the model by reducing overfitting. It balances the trade-off between fitting the data well and keeping the model parameters small. Logistic regression with regularization, such as L1 or L2 regularization (e.g., Lasso or Ridge), can work well for text classification, especially when dealing with a large number of features (words or tokens). Regularization helps prevent overfitting and can improve generalization to some extent. Equation 3876j indicates that the general update rule for θj using the gradient of the loss function is as follows (see page3875): SGD is a gradient-based optimization algorithm that updates the model parameters in small steps to minimize a cost function (in the case of logistic regression, this is typically the log-likelihood or cross-entropy loss) by iteratively adjusting the model's weights. This equation indicates that we need to maximize the log-likelihood. Then, the update rule of θj is given by, To fit a logistic regression model, you typically use a method like maximum likelihood estimation to estimate the coefficients () that maximize the likelihood of the observed data given the model. Once the model is trained, you can use it to make predictions by calculating the probability of an observation belonging to one of the classes and then applying a threshold (usually 0.5) to classify the observation into one of the two classes. Logistic regression is particularly useful when you have a binary outcome variable and want to understand how a set of predictor variables influence the likelihood of an event occurring. It is a linear model, which means it assumes a linear relationship between the independent variables and the log-odds of the binary outcome. If there are more than two classes in the dependent variable, extensions of logistic regression such as multinomial logistic regression or ordinal logistic regression can be used. The probability distribution of the dependent variable in logistic regression follows: 1) A Bernoulli distribution for binary logistic regression. 2) A categorical distribution for multinomial logistic regression. If we have fixed parameters Φ, μ0, μ1, and ε, then we have p(y=1|x; Φ, μ0, μ1, and ε) as a function of x, given by the conditional probability expression, Equation 3876n relates the probability of given ) to the likelihood of observing given ), the prior probability of (), and the marginal probability of (). In this expression, the parameters Φ, are fixed, meaning they are treated as constants and not estimated from data. Under these conditions, the equation can be seen as a representation of Bayesian inference where you are expressing the probability of given as a function of other known probabilities:
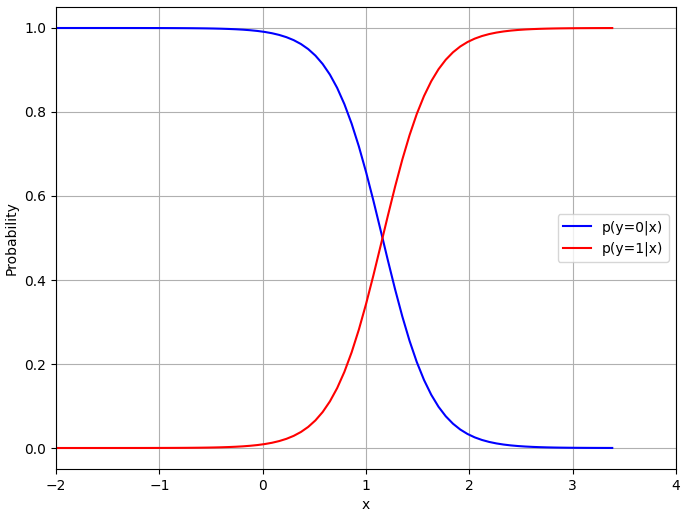
Figure 3876b shows probability density function and probability of logistic regression with fixed Φ, . In Figure 3876b (b) the logistic regression model is used to calculate and over the range of feature values (x).
(a)
(b)
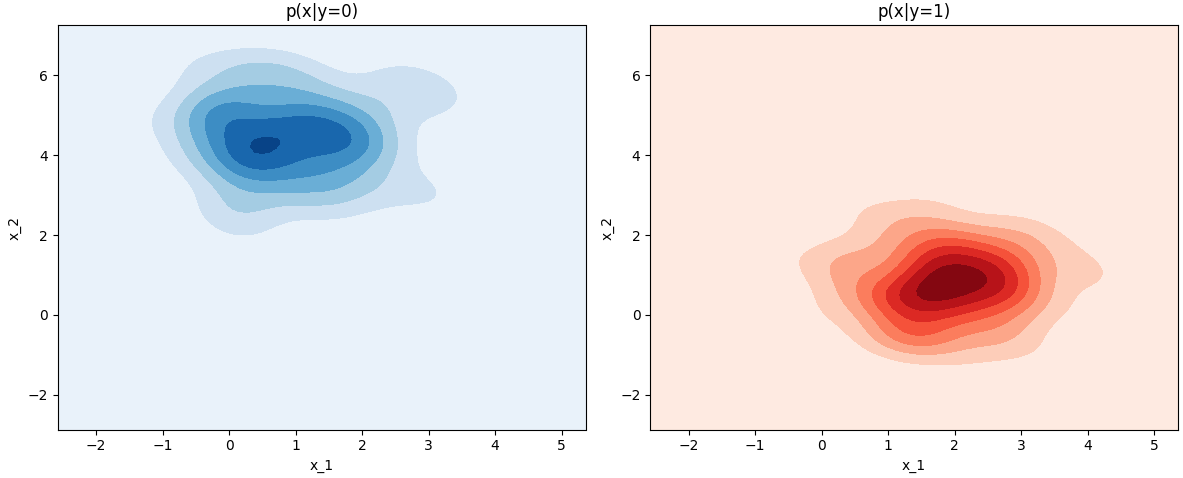
If we have two features, then we will get the probability distributions shown in Figure 3876c.
Figure 3876c. Probability (Python code). As discussed in support-vector machines (SVM), we have, where, g is the activation function. n is the number of input features. With Equations 3876a and 3876o, we can know that the corresponding terms are shown below,
Equation 3876o is a basic representation of a single-layer neural network, also known as a perceptron or logistic regression model, depending on the choice of the activation function g. From Equation 3876o, we can derive different forms or variations by changing the activation function, the number of layers, or the architecture of the neural network as shown in Table 3876a. Table 3876a. Different forms or variations of Equation 3876o.
As an example, assuming we have a dataset s = {x(i), y(i)}, here, i = 1, ..., m. We want to maximize the posterior probability p(θ|S), we can use Bayes' theorem: where, p(s) is a constant. Then, to maximize p(θ|S), we need to maximize p(S|θ) * p(θ), which is, In machine learning, with Gaussian distribution, the prior distribution of θ can be given by, This is a Gaussian (Normal) distribution with mean zero and a covariance matrix of τ2I, where I is the identity matrix. This is a common choice for the prior distribution in Bayesian regularization in machine learning. Table 3876b. Applications and related concepts of logistic regression.
Note that bias, see page3352, in logistic regression model can be introduced. As we know that the logistic regression model predicts the probability that a given input belongs to a particular class. The basic form of logistic regression is: Bias Introduction: If the dataset used to estimate the coefficients β has historical biases or lacks representation from all groups, the model will learn these biases. For example, if a hiring dataset has fewer examples of successful female candidates due to historical biases, the model might undervalue qualifications typically held by women. Mitigation of bias: To avoid this, we can:
============================================
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ================================================================================= | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
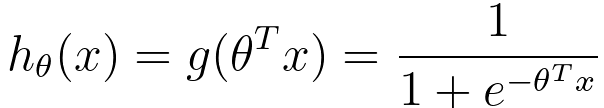 ---------------------- [3876a]
---------------------- [3876a] 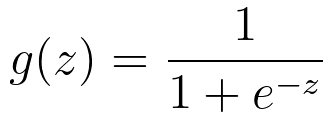 ---------------------- [3876b]
---------------------- [3876b] 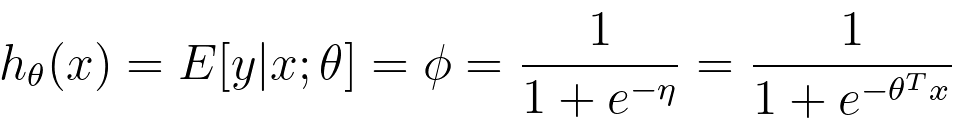 ---------------------- [3876c]
---------------------- [3876c] 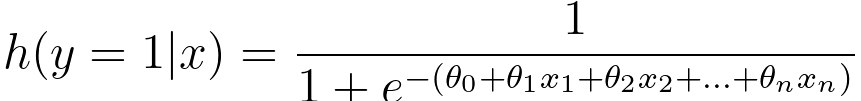 ---------------------- [3876d]
---------------------- [3876d] 
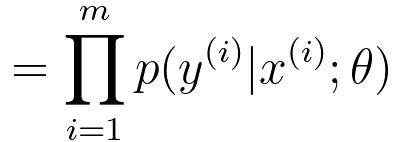 ---------------------- [3876i]
---------------------- [3876i] 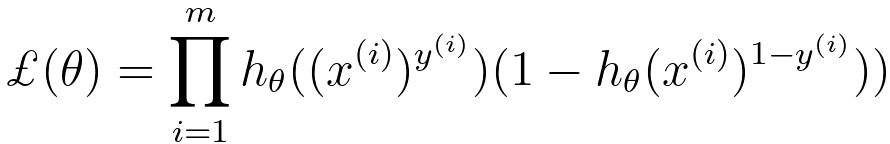 ---------------------- [3876j]
---------------------- [3876j] 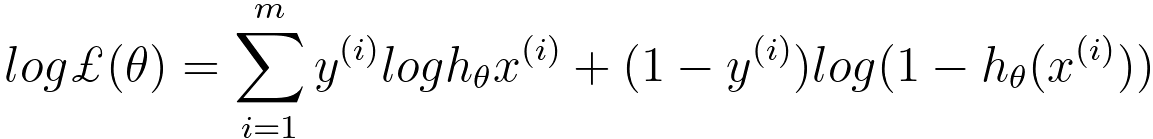 ------------ [3876k]
------------ [3876k]  ---------------------- [3876kb]
---------------------- [3876kb]  ---------------------- [3876kc]
---------------------- [3876kc] 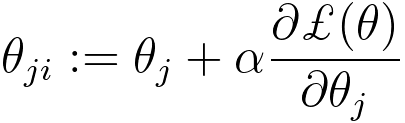 ------------ [3876l]
------------ [3876l] 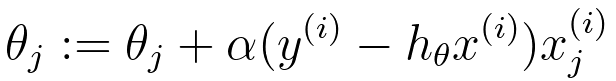 ------------------------ [3876m]
------------------------ [3876m] 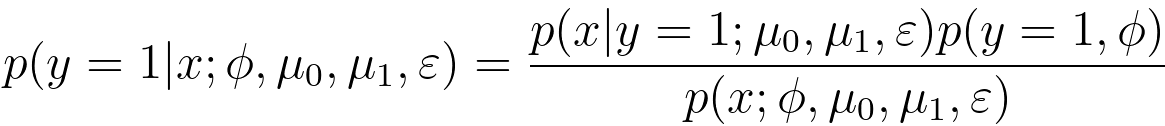 ------------------------ [3876n]
------------------------ [3876n] 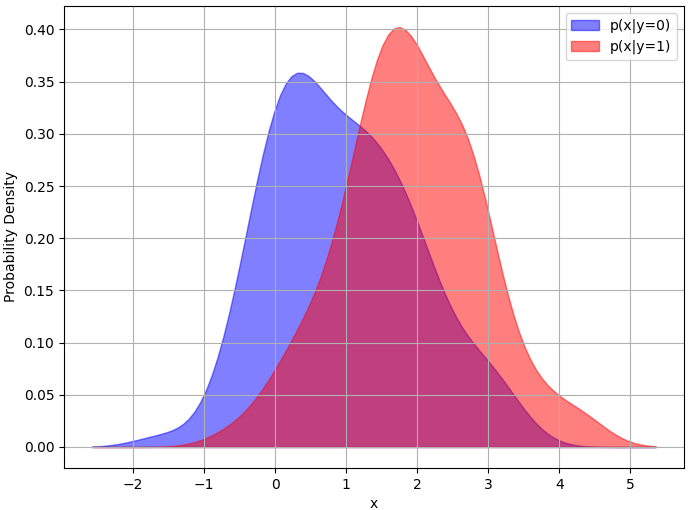
 --------------------------------- [3876o]
--------------------------------- [3876o]  , which is the formula for linear regression.
, which is the formula for linear regression.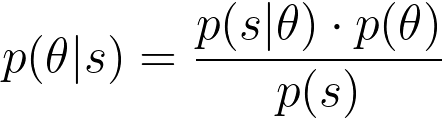 --------------------------------- [3876p]
--------------------------------- [3876p] 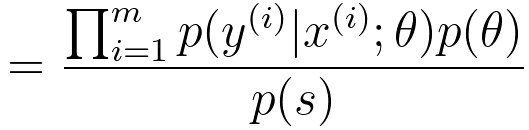 --------------------------------- [3876q]
--------------------------------- [3876q] 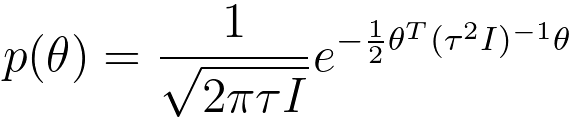 ------------------- [3876r]
------------------- [3876r]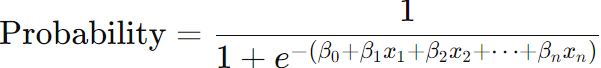 ----------------- [[3876s]
----------------- [[3876s]