Update Parameters θj Using Gradient of Loss Function - Python for Integrated Circuits - - An Online Book - |
||||||||
| Python for Integrated Circuits http://www.globalsino.com/ICs/ | ||||||||
| Chapter/Index: Introduction | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Appendix | ||||||||
================================================================================= In machine learning, when you want to update the parameters θj of a model using the gradient of the loss function ℒ(θ) with respect to θj, you typically use an optimization algorithm such as gradient descent. The update rule for θj is based on the gradient of the loss function and is designed to minimize the loss function over the training data. The general update rule for θj using the gradient of the loss function is as follows: Where:
The idea is to move the parameter θj in the direction that decreases the loss function. The size of the step is controlled by the learning rate α. To update all the parameters of your model simultaneously, you would apply this update rule for each parameter θj in the model. This process is typically repeated for multiple iterations or until a convergence criterion is met (e.g., the change in the loss function becomes very small).
(a)
(b) Figure 3875a. (a) Loss function, and (b) its partial derivative of θ2 (Python script). One example about the updated probability distribution of parameters or hypotheses is that in Bayesian statistics, the posterior distribution, which represents the updated probability distribution of parameters or hypotheses based on observed data, can be given by, P(θ|D) ∝ P(D|θ) * P(θ) ---------------------------------- [3875b] where:
For instance, in neural network, we update: Once the cost function is obtained, we can then plug in the cost function back in the gradient decent update rule and then update the weight parameter. For instance, in machine learning, particularly in the training of neural networks using gradient descent, the process typically involves the following steps:
The gradient descent update rule is generally of the form: ------ [3875d] This process is repeated iteratively until the model converges to a state where the cost function is minimized. In programming, assuming we have a defined gradient_descent function, to plot a graph with weights (w) or parameters (θ) versus cost function, we often need to store each w or θ in a list. On the other hand, for the ML modeling, we only need to return the last w value. To do this, this code is implementing a gradient descent algorithm and plots the cost function over the iterations, and stores each value of w/θ in a list. However, only the last value is stored with reinitialization or overwriting inside a loop so that only the final value is preserved to use in the ML process. ============================================
|
||||||||
| ================================================================================= | ||||||||
|
|
||||||||
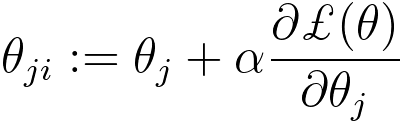 -------------------------------------------- [3875a]
-------------------------------------------- [3875a] 

