=================================================================================
A neural network is a computational model inspired by the structure and functioning of the human brain. It is a fundamental building block in the field of artificial intelligence and machine learning. Neural networks consist of interconnected nodes, known as neurons or artificial neurons, organized into layers. These networks are designed to process information and perform tasks by learning from data.
Here are some key components of a neural network:
-
Neurons: Neurons are the basic processing units in a neural network. Each neuron receives input, processes it, and produces an output. Neurons are often represented mathematically as nodes that perform mathematical operations on their inputs.
-
Layers: Neural networks are typically organized into layers. The three main types of layers are:
- Input Layer: This layer receives the initial data or features to be processed.
- Hidden Layers: These layers are intermediate layers between the input and output layers. They perform complex transformations on the input data.
- Output Layer: This layer produces the final output or prediction based on the information processed in the hidden layers.
-
Weights and Biases: Neurons in a neural network are connected by weighted connections, and each neuron has an associated bias. These weights and biases are parameters that the network learns from training data to make accurate predictions or perform specific tasks.
-
Activation Functions: Neurons apply activation functions to their weighted inputs to introduce non-linearity into the model. Common activation functions include sigmoid, ReLU (Rectified Linear Unit), and tanh (hyperbolic tangent).
-
Forward Propagation: In a neural network, information flows forward from the input layer through the hidden layers to the output layer. This process is called forward propagation, and it involves computing the output of each neuron based on its inputs and activation function.
-
Backpropagation: Neural networks learn from data through a process called backpropagation. During training, the network computes the difference between its predictions and the actual target values (the loss or error). Then, it adjusts the weights and biases using gradient descent optimization to minimize this error. This iterative process updates the network's parameters to improve its performance.
-
Training Data: Neural networks require labeled training data to learn and generalize patterns. The network learns to make better predictions or classifications as it processes more examples during training.
Neural networks have been applied to various machine learning tasks, including image recognition, natural language processing, speech recognition, and many more. Deep learning, a subfield of machine learning, focuses on using deep neural networks with multiple hidden layers to solve complex tasks and has achieved remarkable success in recent years.
Table 4214a. Comparison among different layers in deep learning neural network.
| Application example |
|
Input Layer |
Hidden Layer |
Output Layer |
|
| Feedforward neural network for image classification |
Details |
- Number of Variables: Each pixel in the 28x28 image can be considered a variable. So, there are 28 x 28 = 784 variables in the input layer.
- No activation function is applied in the input layer; it simply passes the pixel values as they are to the next layer.
|
- Number of Nodes: Let's say we have one hidden layer with 128 nodes. The number of nodes in the hidden layer is a hyperparameter that can be adjusted based on the problem and complexity of the task.
- Activation Function: ReLU (Rectified Linear Unit) activation function is commonly used in hidden layers. So, ReLU activation is applied to the output of each node in this layer.
|
- Number of Nodes: In this case, we have 10 nodes in the output layer, where each node corresponds to one of the possible digits (0 through 9). The number of nodes in the output layer matches the number of classes or categories in the classification task.
- Activation Function: Typically, the output layer uses a softmax activation function, especially for multiclass classification problems like this one. The softmax function converts the raw output values into probabilities, where each node represents the probability of the corresponding class.
|
|
| Variables /nodes |
784 variables (no activation function) |
128 nodes (ReLU activation) |
10 nodes (softmax activation) |
|
| Included layers |
|
Convolutional Layer (CONV)
Pooling Layer (e.g., MaxPooling)
Convolutional Layer (CONV)
Pooling Layer
Fully Connected Layer (FC) |
|
|
| Energy usage |
|
99% energy are used by Convolutional Layer (CONV) and Fully Connected Layer (FC) |
|
|
| * Feedforward neural network for image classification: this builds a neural network to classify handwritten digits from the MNIST dataset, where each image is a 28x28 pixel grayscale image of a handwritten digit (0 through 9). |
Fitting a neural network involves training it on a dataset so that it can learn to make accurate predictions or classifications. Here are the general steps to fit a neural network:
-
Data Preparation:
Data Collection: Gather and organize your dataset. Ensure you have labeled data, with input features and corresponding target labels.
-
Data Preprocessing: Clean and preprocess your data. This may involve tasks such as normalization, feature scaling, handling missing values, and encoding categorical variables.
-
Data Splitting: Split your dataset into training, validation, and test sets. The training set is used to train the model, the validation set helps tune hyperparameters and monitor training progress, and the test set is used for final evaluation.
-
Model Architecture:
- Decide on the architecture of your neural network, including the number of layers, the number of neurons in each layer, and the choice of activation functions. This is a crucial step, and it often requires experimentation to find the best architecture for your specific problem.
-
Initialization:
- Initialize the weights and biases of your neural network. Common initialization methods include random initialization and Xavier/Glorot initialization.
-
Loss Function:
- Choose an appropriate loss function (also known as a cost or objective function) that measures the difference between the model's predictions and the true target values. The choice of loss function depends on the type of problem (e.g., regression, classification) and the output layer's activation function.
-
Optimizer:
- Select an optimization algorithm, such as stochastic gradient descent (SGD), Adam, or RMSprop. The optimizer adjusts the model's weights and biases during training to minimize the loss function.
-
Training Loop:
- Iterate through the training data in mini-batches:
- Forward Propagation: Pass a mini-batch of input data through the network to make predictions.
- Compute the Loss: Calculate the loss using the chosen loss function and the predictions.
- Backpropagation: Calculate gradients of the loss with respect to the network's parameters (weights and biases) using backpropagation.
- Update Parameters: Use the optimizer to update the model's parameters based on the gradients.
- Repeat these steps for multiple epochs (iterations over the entire training dataset) until the model converges.
-
Hyperparameter Tuning:
- Experiment with different hyperparameters, such as learning rate, batch size, the number of epochs, and regularization techniques (e.g., dropout) to find the best combination that results in good model performance.
-
Validation:
- Periodically evaluate the model on the validation set to monitor its performance and detect overfitting. Adjust the model or training parameters if necessary.
-
Testing:
- Once you are satisfied with the model's performance on the validation set, evaluate it on the test set to get an unbiased estimate of its generalization performance.
-
Deployment:
- If the model meets your requirements, you can deploy it in a real-world application to make predictions or classifications on new, unseen data.
Remember that fitting a neural network can be an iterative process, involving experimentation with different architectures, hyperparameters, and data preprocessing techniques to achieve the best results for your specific task.
============================================
One example of neural networks is autoencoder. Regarding data compression via autoencoders, we can think about such examples. Assuming that a program is created to send some data from one PC to another. The data is a collection of data points, each has two dimensions as shown in Figure 4214a. Since the network bandwidth is limited, every bit of data which is going to be sent should be optimized. When sending the data, instead of sending all the data points, we can send only the first dimension of every data point to the other PC, and then at the other PC, we compute the value of the second dimension with the linear relationship from the first dimension. This method requires some computation, and the compression is lossy, but it reduces the network traffic by ~50%.

Figure 4214a. Data to be sent from one PC to another PC. The blue dots represent the data points. The horizontal axis is the value of the first dimension, while the vertical axis is the value of the second dimension. |
The problem above is two-dimensional (2D). If the data is high-dimensional, then the set of data points can be given by {a(1), a(2), ..., a(m)}, where each data point has many dimensions. Therefore, a method is needed to map the points to another set of data points {z(1), z(2), ... , z(m)}, where z’s have lower dimensionality than a’s and a’s can faithfully reconstruct a’s.
Recall that sending the data from one PC to another includes the steps below:
i) Encoding on the first PC. Map the original data a(i) to the compressed data z(i).
ii) Sending the data z(i) to the second PC.
iii) Decoding the data. Map the compressed data z(i) back to ã(i), which approximates the original data a(i).
Therefore, the following equations can be obtained:
z(i) = W1a(i) + b1 ------------------------------------------------------------------------------------ [4214a]
ã(i) = W2z(i) + b2 ------------------------------------------------------------------------------------ [4214b]
In practice, if a(i) is a two-dimensional vector, it can be possible to visualize the data to find W1, b1 and W2, b2 analytically. However, in most cases, it is difficult to find those matrices using
visualization only; therefore, gradient descent is needed. As the goal is to have ã(i) is approximately equal to a(i), thus the sum of squared differences between is given by objective function,
 --------------------------------------------------- [4214c] --------------------------------------------------- [4214c]
 ------------------------ [4214d] ------------------------ [4214d]
which can be minimized using stochastic gradient descent.
As discussed in support-vector machines (SVM), we have,
 --------------------------------- [4214e] --------------------------------- [4214e]
where,
g is the activation function.
n is the number of input features.
Equation 4214e is a basic representation of a single-layer neural network, also known as a perceptron or logistic regression model, depending on the choice of the activation function g. From Equation 4214e, we can derive different forms or variations by changing the activation function, the number of layers, or the architecture of the neural network as shown in Table 4214b.
Table 4214b. Different forms or variations of Equation 4214e.
| Algorithms |
Details |
| Linear Regression |
Set g(z) = z (identity function).
This simplifies the equation to  , which is the formula for linear regression. , which is the formula for linear regression. |
| Logistic Regression |
Set g(z) = 1 / (1 + e(-z)) (the sigmoid function).
This is a binary classification model, and the equation becomes the logistic regression model. |
| Multi-layer Neural Network |
You can add more layers to the network by introducing new sets of weights and biases, and applying activation functions at each layer. This leads to a more complex model. |
| Different Activation Functions |
You can choose different activation functions for different characteristics of your model. For example, you can use ReLU, tanh, or other non-linear activation functions instead of the sigmoid function. |
| Deep Learning Architectures |
You can create more complex neural network architectures, such as convolutional neural networks (CNNs) for image data or recurrent neural networks (RNNs) for sequential data. |
| Regularization |
You can add regularization terms, such as L1 or L2 regularization, to the loss function to prevent overfitting. |
This particular architecture above is also known as a linear autoencoder as shown in the
network architecture in Figure 4214b. In the case in the figure, we are trying to map data from 8 dimensions to 4 dimensions using a neural network
with one hidden layer z.

Figure 4214b. Linear autoencoder.
One-hot-encoding is a process by which categorical variables are converted into a form that could be provided to neural networks to do a better job in prediction.
Sequential API can be used to create a Keras model with TensorFlow (e.g. on Vertex AI platform). Then, the Keras Sequential API and Feature Columns can be used to build deep neural network. In combination with a trained model, the Keras model can be saved, loaded and deployed, and then the model can be called for making predictions.
A deep neural network trained on this data would be recommended to be used if you have lots of images of different types of things labeled with their species name, and lots of computational resources.
It is also possible to apply regularization techniques to individual elements of model parameters, especially in neural networks and deep learning. The choice of regularization technique depends on the problem at hand and the characteristics of your data and model. It's common to experiment with different regularization methods and hyperparameters to find the best regularization strategy for your specific task. Regularization helps improve the generalization performance of your model by reducing the risk of overfitting. Table 4214c lists the common regularization techniques for neural network parameters.
Table 4214c. Common regularization techniques for neural network parameters.
| Regularization |
Details |
| L1 Regularization (Lasso) |
L1 regularization encourages sparse weight vectors by adding the absolute values of the weights as a penalty to the loss function. This can lead to some weights becoming exactly zero, effectively pruning the network. |
| L2 Regularization (Ridge) |
L2 regularization adds the squared values of the weights as a penalty to the loss function. It encourages smaller weight values and helps prevent large weight magnitudes that could lead to overfitting. |
| Elastic Net Regularization |
Elastic Net is a combination of L1 and L2 regularization, allowing you to apply both penalties simultaneously. It can be useful when you want a balance between sparsity and weight decay. |
| Weight Decay |
Weight decay is another term for L2 regularization, and it refers to the practice of adding the L2 penalty to the loss function. This helps control the magnitude of the weights. |
| Group Lasso |
Group Lasso is a form of L1 regularization applied to groups of related parameters. It encourages sparsity among groups of parameters rather than individual weights. This is often used when there is some inherent grouping or structure in the parameters, like convolutional filters in a CNN. |
| DropConnect |
Similar to dropout, DropConnect randomly sets individual weight connections to zero during training, which regularizes the network by making it less reliant on specific weights. |
| Weight Clipping |
Weight clipping involves bounding the values of weights to a specific range during training. This can help prevent the growth of excessively large weights and mitigate exploding gradient problems. |
For the dog classification problem described in page4324, for a single dog image, we have,
| X is a 64 x 64 image |
|
There are 64x64x3 x since there are 64 x 64 pixels and 3 colors in the image, namely 12,288 x 1 matrix |
|
Logistic regression can be used: y^ = (1, 1) matrix, w = 1 x 12,288 matrix, and x = 12,288 x 1 matrix |
| There are 12,289 parameters in this problem (12,288 weights and 1 bias). Note that the number of the parameters depends on the size of the image. |
 |
|
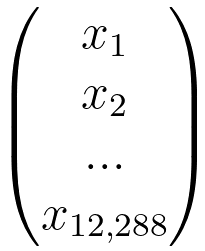 |
 |
|
|
Neuron = linear + activation |

 |
| = |
a |
→ |
wx+b | σ |
This is called as forward propagation.
| The shapes of the parameters are: z[1] is (3,1), w[1] is (3, n), x is (n, 1), a[1] and b[1] is (3, 1), z[2] and b[2] is (2, 1) because there are 2 neurons in the second layer, w[2] is (2, 3), a[2] is (2, 1), z[3] and a[3] is (1, 1), w[3] is (1, 2) and b[3] is (1, 1). These numbers are very helpful, especially when coding. |
| |
|
|
|
Input 1 = a1(1), Output 1 = a1(3), and so on. All the blue circles represent neurons. |
 |
= |
 |
 |
 |
→ |
y^ |
| |
|
|
|
| Stack 3 neurons |
Stack 2 neurons |
|
Stack the 3 layers |
Parameters in each layer: |
w[1], b[1] |
w[2], b[2] |
w[3], b[3] |
| Increasing the number of layers and parameters can enhance the model's capacity to capture complex patterns in data. The key is to design a network architecture that is well-suited to the complexity of the data we are working with. We need to train all the parameters in each layer. |
Updates: |
|
|
|
|
The diagram above describes a neural network architecture. The input layer has 3n + 3 parameters, the hidden layer has 2 x 3 weights + 2 biases, and the output layer has 2 x 1 + 1 bias. That means not many parameters are added because of the neural network, since most parameters are the original ones. The first layer (input layer) is responsible for understanding the fundamentals of a dog image, specifically detecting edges. This layer may learn basic features like edges, corners, ear, mouse, or textures, and subsequent layers learn to combine these features to recognize higher-level patterns. The idea is that neurons in the input layer are designed to detect certain features (in this case, edges), and these features are then communicated to neurons in the next layers.
In edge detection of images in a convolutional neural network (CNN), each neuron in the first layer corresponds to a small local receptive field in the input image. This receptive field is essentially a small region defined by the dimensions of the convolutional filter or kernel. When a neuron in the first layer processes an input, it does so by applying a convolution operation. This operation involves taking the element-wise product of the filter weights and the corresponding pixel values in the receptive field and then summing up these products. This sum is then passed through an activation function. filters can be designed to respond to specific patterns in the input, such as changes in intensity or color. For example, a simple edge detection filter might have positive weights on one side and negative weights on the other. When this filter is convolved with an image, it responds strongly to areas where there is a sharp transition in intensity, indicating the presence of an edge. The network checks whether nearby pixels have similar colors or not. The convolutional operation, combined with weight multiplication and activation functions, allows the network to learn to detect and respond to different features in the input, including edges. As the network goes through training, the weights in these filters are adjusted to capture the patterns and features relevant to the task at hand.
For an input batch of m examples (e.g. m dog images), we then have,
The round brackets, (1) , (2), ..., (m), are for the images. |
Since we have more layers, we want to run the codes in parallel.
For the case with the m examples, we then have,
Z[1] = w[1] X + b[1]
 -------------------------------- [4214f] -------------------------------- [4214f]
Then, the shapes of Z[1] is (3, m) and X is (m, m), w[1] is (3, n).
Because we do not want to add unnecessary parameters in computation, we use some technique, called broadcasting, for b[1]:
 -------------------------------- [4214g] -------------------------------- [4214g]
With broadcasting, we just repeat the same parameter in order to be able to write our code in parallel. In Python, there is a library, called NumPy (numerical Python) to code these equations. With this NumPy package (code), we can directly do broadcasting.
The cost function can be given by (see Forward and Backward Propagations),
 ---------------------------------------- [4214h] ---------------------------------------- [4214h]
Now, we can plug in the cost function back in the gradient decent update rule and then update the weight parameter. However, after forward and backward propagations, the network is not good enough so that the performance of the neural network needs to be improved by using various strategies:
i) Using different activation functions can be a strategy for improving neural network performance. Experimenting with different activation functions is a valid approach during the model development process. However, the choice of activation function should be guided by the specific characteristics of the problem at hand, the nature of the data, and empirical observations during experimentation.
ii) Normalizing the input in a neural network can be beneficial for several reasons, including avoiding saturation issues when the input values (z) are too large or too small. The same normalization needs to be applied in both train set and test set.
iii) It could involve adjusting hyperparameters, changing the network architecture, adding regularization techniques, increasing the amount of training data, or fine-tuning other aspects of the training process.
iv) Neural networks usually require multiple iterations (epochs) of training to learn complex patterns in data.
Table 4214d. Applications and related concepts of neural network.
| Applications |
Page |
| Soft Margin versus Hard Margin |
Introduction |
Table 4214e. Deep learning libraries.
============================================
|

 --------------------------------------------------- [4214c]
--------------------------------------------------- [4214c] ------------------------ [4214d]
------------------------ [4214d] --------------------------------- [4214e]
--------------------------------- [4214e]  , which is the formula for linear regression.
, which is the formula for linear regression.










 -------------------------------- [4214f]
-------------------------------- [4214f]  -------------------------------- [4214g]
-------------------------------- [4214g]  ---------------------------------------- [4214h]
---------------------------------------- [4214h]