| The point group of a diffraction pattern is often called “Laue class” of the diffraction pattern. Table 3020 shows the relationship between Laue classes and point groups.
Table 3020. Relationship between Laue classes and point groups.
| System |
Essential symmetry |
Lattice symmetry |
Symmetry equivalent reflections * |
Laue class (Diffraction symmetry) |
Point Groups (Hermann–Mauguin notation) |
| Triclinic |
None |
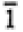 |
2: hkl, -h-k-l |
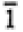 |
1, -1 |
| Monoclinic |
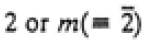 |
2/m |
4: hkl, -h-k-l, h-kl, h-kl |
2/m |
2, m, 2/m |
| Orthorhombic |
222 or 2mm
|
mmm
|
8: hkl, -h-k-l, h-kl, h-kl,
-hkl, hk-l, -h-kl, h-k-l |
mmm |
222, mm2, mmm |
| Tetragonal |
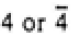 |
4/mmm
|
8: hkl, -h-k-k, khl, -k-h-l,
hk-l, -h-kl, kh-l, -k-hl |
4/m
|
4, -4, 4/m |
| 16: |
4/mmm |
422, -42m, 4mm, 4/mmm |
| Trigonal |
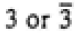 |
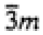 |
6: |
3 |
3, -3 |
| 12: |
-3m1 |
321, 3m1, -3m1 |
| 12: |
-31m |
312, 31m, -31m |
| Hexagonal |
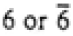 |
6/mmm
|
12: |
6/m |
6, -6, 6/m |
| 24: |
6/mmm |
622, -62m, 6mm, 6/mmm |
| Cubic |
23 |
m3m
|
24: |
m-3 |
23, m-3 |
| 48: |
m-3m |
432, -43m, m-3m |
| * Symmetry equivalent reflections: All of them have the same intensity. |
|
