=================================================================================
The aberration determination method based on diffractogram is the most effective method and takes advantage of the fact that for a thin amorphous TEM sample the diffractogram is directly related to the phase Contrast Transfer Function (pCTF) and thus all the zero crossings in the pCTF will show up as dark rings. This method is employed where theoretically calculated and experimental diffractograms are matched. Note different from the technique based on tilting the illumination this method is insensitive to sample drift. The disadvantage of this method is that it is not possible to do the aberration extraction when strong reflections from crystalline material mask the amorphous signal. However, in many cases, although the crystalline reflections have higher intensity than the amorphous signal they are limited to a smaller area in the diffractogram and thus the phase (but not the amplitude) of the entire diffractogram can still be approximately described by a weak phase amorphous object. Moreover, this is still true for many complicated crystalline materials due to a thin, disordered layer on the two surfaces of milled TEM samples or the carbon support films on the TEM grids (e.g. for the nanoparticle case). Therefore, this method is almost applicable to all materials.
In this method, in the first step of the process of aberration evaluation, two images are compared using a phase correlation function (PCF) with a trial function, t, containing an estimated defocus difference, Δf2 - Δf1 (ΔC1), between the two images. When this estimation is correlated to the actual defocus difference the PCF collapses to a single peak at a position,
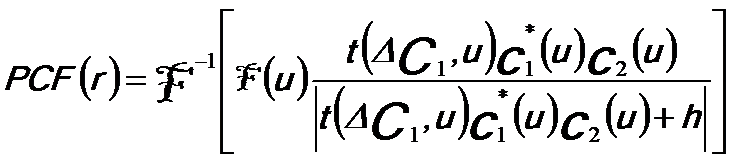 --------------- [3682a] --------------- [3682a]
Here, low case c1 and c2 represents the two images, F(u) is used to minimize the effects of high frequency noise, and h simply prevents a zero denominator. The result from the PCF is then used in the second trial function. Furthermore, the phase contrast index (PCI) calculates the absolute values of aberration coefficients A1 (twofold astigmatism) and C1 (defocus) and together with the spherical aberration.
The procedure of the aberration measurement here employs the fact that the phase shift of an uncorrected system depends on the direction of the illumination plane wave. Therefore, a tilt of the illumination beam changes the coefficients of the expansion of the phase shift in a Taylor series with respect to the scattering angle. Figure 3682 shows the procedure that the determination of aberration is carried out by recording a Zemlin tableau of diffractograms from an amorphous area of a specimen [1, 2]. The lens defocus is first preset to a certain underfocus to generate Thon rings. In order to obtain a series of diffractograms, the illumination is intentionally tilted. In other words, those different diffractograms are obtained from the images taken with parallel illumination and at two tilt angles and several azimuthal angles. The entire set of diffractograms is so-called diffractogram tableau. The aberration coefficients are calculated from the coefficients derived from the diffractograms. By measuring the induced first-order aberrations of individual defocus and twofold astigmatism, the true aberrations of the imaging system are obtained. The obtained diffractogram is compared with a database of Thon ring patterns for a wide range of defocus and twofold astigmatism [3]. A computer is employed to control the procedure of aberration measurement and to drive the camera and the illumination system of the microscope. By utilizing the data derived from the diffractograms, the computer can obtain the target voltages and currents that are necessary to compensate for the misalignment aberrations. Subsequently the values of the obtain voltages and currents are applied through a computer-controlled power supply unit to the electrodes and coils of the various stigmators in the microscope.
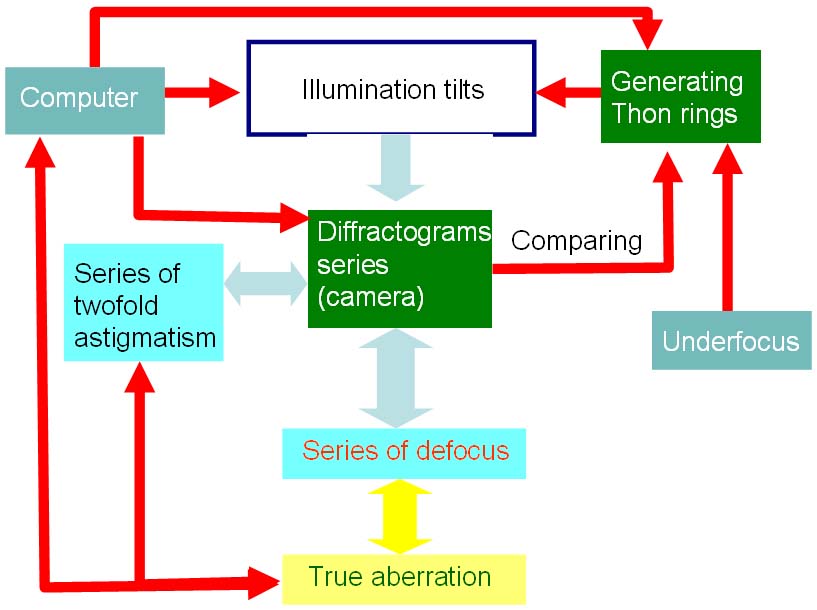
Figure 3682. Procedure of aberration determination based on diffractogram.
In the aberration measurement method based on diffractogram, the prerequisite is an accurate determination of defocus and twofold astigmatism from each diffractogram. A constant defocus must presents over the field of view on the thin amorphous area used to record diffractograms. Any defocus change, e.g. induced by a wedged or other non-uniform thickness in the TEM film, results in a defocus spread affecting the quality of the Thon ring pattern and deteriorate the high-frequency information that is needed for accurate aberration measurement.
Due to the constrain of the defocus spread caused by contributions from upper and lower faces of the specimen and atomic planes inside the specimen, the maximum thickness of the thin amorphous area for the aberration measurement should be equal to the defocus spread, given by,
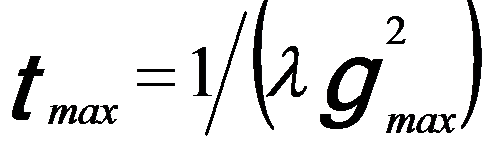 --------------- [3682b] --------------- [3682b]
Note that in order to avoid blurring and streaking in reciprocal space, the amorphous area with uniform thickness should be large enough. In many cases, one has to use the thin amorphous material induced by specimen preparation; unfortunately, those areas normally are too thick or are shaped in stripes.
[1] Zemlin, F., Weiss, K., Schiske, P., Kunath, W. & Herrmann,
K.-H. (1978). Coma-free alignment of high-resolution electron
microscopes with the aid of optical diffractograms. Ultramicroscopy
3, 49–60.
[2] Typke, D. & Dierksen, K. (1995). Determination of image aberrations
in high-resolution electron microscopy using diffractograms
and cross-correlation methods. Optik 99, 155–166.
[3] Uhlemann, S. & Haider, M. (1998). Residual wave aberrations in
the first spherical aberration corrected transmission electron
microscope. Ultramicroscopy 72, 109–119.
|
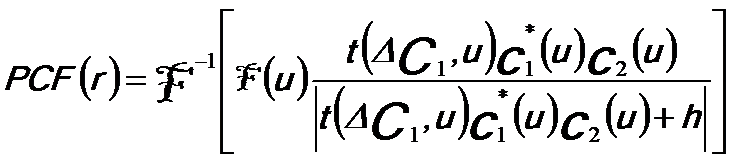 --------------- [3682a]
--------------- [3682a] 