=================================================================================
Certain lattice, such as body centered cubic (Cubic I) and face centered cubic (Cubic F), have "kinematically" forbidden reflections. In other words, due to the arrangements of the atoms in the unit cell, these are reflections where the intensity of the scattered wave is zero, given by,
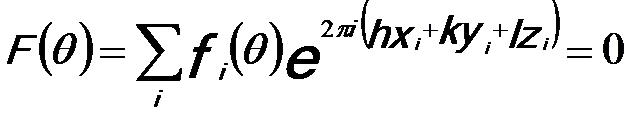 ---------------------------- [3897] ---------------------------- [3897]
where,
xi, yi, and zi -- The positions of the atoms in the unit cell.
Those reflections are destructive and thus they do not show up in the diffraction patterns, however, the relevant crystalline planes certainly exist in the crystals.
Table 3897a lists the symmetry elements that cause systematic forbidden reflections.
Table 3897a. Symmetry elements that cause systematic forbidden reflections.
The reflections that are kinematically forbidden due to the presence of screw axes or glide planes will appear in the diffraction pattern of a crystal that scatters dynamically. However, the kinematically forbidden reflections due to unit-cell centering [2] do not show in the dynamical scattering.
Table 3897b. Conditions of forbidden and allowed reflections (h k l)
of common crystal structures
(F: the Structure Factor).
Bravais Lattice |
Forbidden reflections |
Allowed reflections |
F |
Number of lattice points
per cell |
Example Compounds |
Primitive Cubic |
None |
Any h, k, l |
f |
1 |
α-Po |
fcc |
h, k, l are mixed odd and even |
h, k, l are all odd or all even |
4f |
4 |
fcc metals, GaAs, NaCl-rocksalt, ZnS-zincblende |
bcc |
h + k + l is odd |
h + k + l is even |
2f |
2 |
bcc metals |
fcc |
h, k, l are mixed odd and even; or, all even and h + k + l ≠ 4n |
As fcc, but if all even and h + k + l ≠ 4n, then absent (n is integer)
|
|
|
Si, Ge, Sn - diamond cubic |
Base centered |
|
h, k and l all odd or all even |
2f |
2 |
|
|
h + k + l is odd
|
|
|
|
bct |
Primitive Hexagonal |
h + 2k = 3m and l is odd |
All other cases |
|
|
Hexagonal closed packed (hcp) metals |
Hexagonal close-packed (hcp) |
|
|
|
Reflection example |
|
| |
h + 2k = 3n with l odd |
0 |
0001 |
|
| |
h + 2k = 3n with l even |
2f |
0002 |
|
| |
h + 2k = 3n ± 1 with l odd |
f3 |
01-11 |
|
| |
h + 2k = 3n ± 1 with l even |
f |
01-10 |
|
For hcp crystals, the (0 0 0 l) reflections, e.g. for the case with 164 (P-3m1) space group, are forbidden when l is odd. However, those reflection positions often show diffraction intensity, which is probably caused by chemical order on the basal planes, or by double or multiple diffraction (scattering).
Table 3897c. Miller indices of diffracting planes, and allowed and forbidden reflections.
| {hkl} |
Σ[h2 + k2 + l2 ] |
FCC |
Diamond cubic |
BCC |
| {100} |
1 |
- |
- |
- |
| {110} |
2 |
- |
- |
110 |
| {111} |
3 |
111 |
111 |
- |
| {200} |
4 |
200 |
200 |
200 |
| {210} |
5 |
- |
- |
- |
| {211} |
6 |
- |
- |
211 |
| |
7 |
- |
- |
- |
| {220} |
8 |
220 |
220 |
220 |
| |
9 |
- |
- |
- |
| {310} |
10 |
- |
- |
310 |
{311}
|
11 |
311 |
331 |
- |
| {222} |
12 |
222 |
- |
222 |
| |
13 |
- |
- |
- |
| {321} |
14 |
- |
- |
321 |
| |
15 |
- |
- |
- |
| {400} |
16 |
400 |
400 |
400 |
| |
17 |
- |
- |
- |
| {411} |
18 |
- |
- |
411 |
| {330} |
18 |
- |
- |
330 |
| {331} |
19 |
331 |
331 |
- |
| {420} |
20 |
420 |
- |
420 |
| |
21 |
- |
- |
- |
| {332} |
22 |
- |
- |
332 |
| |
23 |
- |
- |
- |
| {422} |
24 |
422 |
422 |
422 |
| |
25 |
- |
- |
- |
| {431} |
26 |
- |
- |
431 |
| {511} |
27 |
511 |
511 |
- |
| {333} |
27 |
333 |
333 |
- |
| |
28 |
- |
- |
- |
| |
29 |
- |
- |
- |
| {521} |
30 |
- |
- |
521 |
| |
31 |
- |
- |
- |
| {440} |
32 |
440 |
440 |
440 |
Table 3897d. Forbidden and allowed reflections (h k l)
of some materials.
Lattice |
Examples of forbidden reflections |
Examples of allowed reflections |
Example Compounds |
Cubic perovskite structure |
{1 0 0} |
|
SrTiO3 |
For symmetry determination with both XRD and electron diffraction crystallography, we are looking for symmetry-related reflections. Then, the difference between the two techniques is mainly on systematically forbidden reflections:
i) In XRD profiles, the forbidden reflections typically have absolutely zero intensity.
ii) In SAED patterns, such forbidden reflections always have some degree of intensity due to double diffraction from multiple scattering.
Therefore, in SAED analysis, to minimize the multiple scattering, we need to use extremely thin specimens. Fortunately, precession electron diffraction (PED) gives an opportunity to provide closer kinematical conditions and are less dynamical than SAED. Given a large precession angle, the kinematical forbidden reflections can be identified [1]. However, in most cases, the forbidden reflections in PED patterns will not be fully absent since the patterns are produced as a sum of many misaligned electron diffraction patterns and screw axes can only be completely absent if the zone axis of the crystal is perfectly aligned.
Furthermore, for CBED patterns, we have:
i) The odd order reflections in the direction of the axis will be forbidden if the glide plane is parallel to the electron beam.
ii) For a screw axis or glide plane, if the projection of the unit cell in the beam direction has a symmetry, then the forbidden reflections would not be fully forbidden but would obviously be very weak.
[1] J. P. Morniroli, A. Redjaïmia, S. NIcolopoulos, Ultramicroscopy 107
(2007) 514.
[2] D. E. Sands. Introduction to crystallography. Dover Publications, 1993.
|