=================================================================================
The cross section of inelastic scattering of an electron, when divided by the actual area of an atom, gives the probability that a scattering event will occur.
The inelastic cross section can be well described by Fermi’s Golden Rule so that the differential scattering cross section (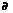 σ/ σ/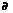 Ω) can be given by, Ω) can be given by,
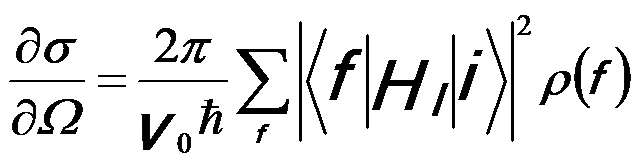 ----------------- [4436a] ----------------- [4436a]
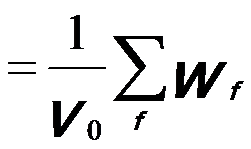 = ----------------- [4436b] = ----------------- [4436b]
where,
Ω -- The solid angle,
|i> -- The initial state (consisting of the wave
functions of the incident electron and of the electrons in the atoms),
<f| -- The final state (consisting of the atomic electron wave function of the electrons in the atoms and the exit plane wave at nearly the same energy as the incident energetic electron),
wf -- The transition rate from an initial state to a final state <f|,
ħ -- The Planck’s constant divided by 2π,
v0 -- The
velocity of the incident electron,
ρ(f) -- The density of final states of the high-energy scattered electron (per unit energy per solid angle),
HI -- The
interaction Hamiltonian.
The expression in Equations 4436a and 4436b includes the sum over all allowed final atomic states.
On the other hand, according to the conservation of energy constraint, if the high-energy electron is incident on an atom with a nuclear charge of Ze and Z internal electrons then the interaction Hamiltonian can be given by,
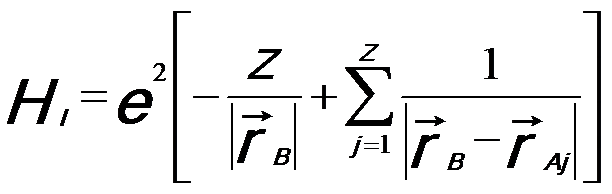 ----------------- [4436c] ----------------- [4436c]
where,
rAj -- The positions of the atomic spatial coordinates
of the atomic electrons,
rB -- The position of the incident electron beam,
e -- The electron charge
(e > 0).
In Equation 4436c, the origin (r=0) is set at the nucleus of the atom. The first term is the interaction of the incident electron beam with
the nucleus and the second term is the interaction
with the bound electrons in the atom.
In other words, the cross section of inelastic electron scattering represents the energy losses of incident electrons traveling in solids. The function of the cross section depends on the energy of the electron interacting with the solids, its trajectory, and the dielectric properties of the medium interacted.
According to the dielectric response theory, the electron inelastic differential cross section can be given by [1 - 3],
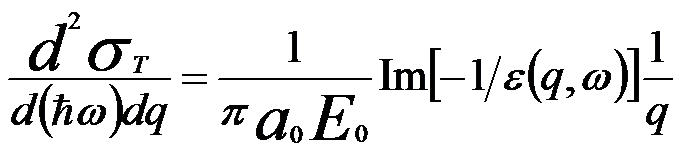 ------ [4436d] ------ [4436d]
where,
E0 -- Kinetic energy of the incident electron
a0 -- Bohr radius
ħω -- Energy loss from the incident electron into a medium described by the dielectric response function ε(q, ω)
ħq -- Momentum transfer from the incident electron into a medium described by the dielectric response function ε(q, ω)
Equation 4436d determines the probability of an inelastic scattering event, the energy loss distribution, and the scattering angular distribution. Then, the inelastic scattering cross section for electrons traveling in an infinite medium can be given by,
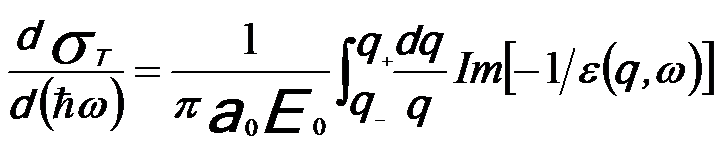 ------ [4436e] ------ [4436e]
where,
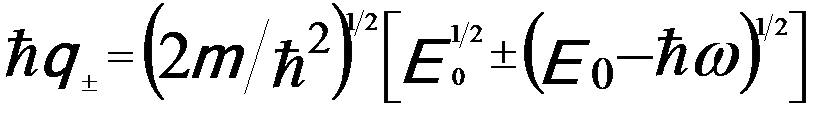 ------ [4436f] ------ [4436f]
ħq± are the maximum and minimum momentum transfer allowed by the energy and momentum conservation laws. For weak momentum transfer (ħq), the dependence of ε on q is also weak compared with 1/q, so the general shape of dσT/d(ħω) is given as a first approximation by the energy-loss function (ELF) Im(-1/ε) and thus the ELF determines the low energy losses of electrons traveling in the bulk of a solid.
The quantity Im[-1/ε(q,ω)] is commonly referred to as the energy loss function. Therefore, the stopping power (SP, dE0/dS) and the mean free path (MFP, λ) can be obtained and given by [4],
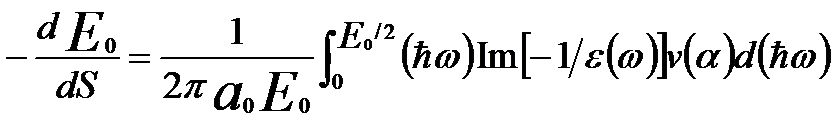 ------ [4436g] ------ [4436g]
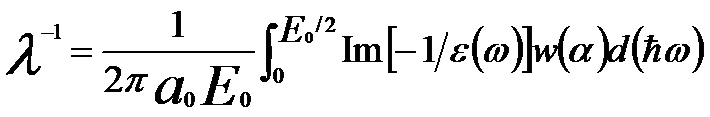 ------ [4436h] ------ [4436h]
If an electron traveling through a thin foil (e.g. a thin TEM sample), the corresponding inelastic scattering cross section is given by, [5 - 7]
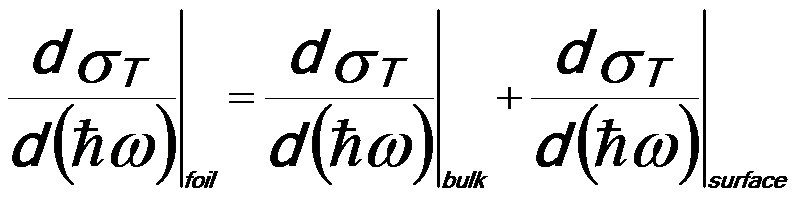 ------------ [4436i] ------------ [4436i]
dσT/d(ħω)|surface presents the surface contribution to the total energy losses of the incident electrons, and in principle is a complicated function of ε, the foil thickness t, and the incident angle α of the primary electron beam with respect to the surface normal of the foil. These surface excitations are generally induced within a few angstroms at the surface of the foil between the foil and the vacuum. The depth of this “surface region” has a physical extension that increases with the square root of the energy of the incident electrons (E0).
[1] Lindhard J (1954) On the properties of a gas charged of particles.
K Dan Vidensk Selsk Mat Fys Medd 28:1–57
[2] Ritchie RH (1959) Interaction of charged particles with a degenerate
Fermi-Dirac electron gas. Phys Rev 114:644–654
[3] Pines D, Nozieres P (1966) The theory of quantum liquids.
Benjamin, New York
[4] Zhenyu Tan, Yueyuan Xia, Mingwen Zhao, and Xiangdong Liu, Electron stopping power and inelastic mean free path in amino acids and protein over the energy range of 20–20,000 eV, Radiat Environ Biophys (2006) 45: 135–143.
[5] R. H. Ritchie, Phys. Rev. 106, 874 (1957).
[6] E. A. Stern and R. A. Ferrel, Phys. Rev. 120, 130 ~1960!; A. Otto, Phys. Status Solidi 22, 401 (1967).
[7] H. Raether, in Excitation of Plasmon and Interband Transitions by Electrons, edited by G. Ho¨hler, Springer Tracts in Modern Physics Vol. 88 (Springer, New York, 1980).
|
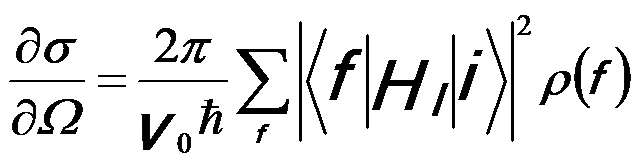 ----------------- [4436a]
----------------- [4436a]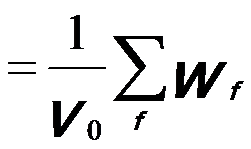 = ----------------- [4436b]
= ----------------- [4436b] 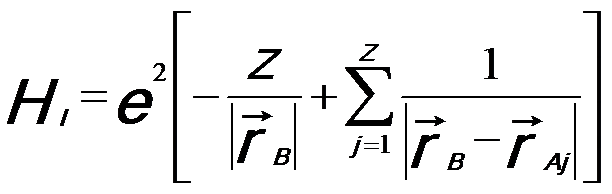 ----------------- [4436c]
----------------- [4436c]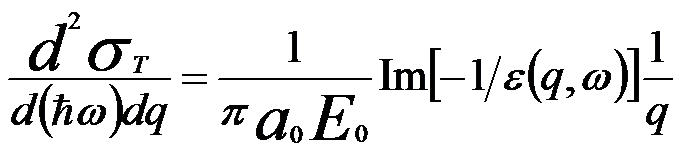 ------ [4436d]
------ [4436d] 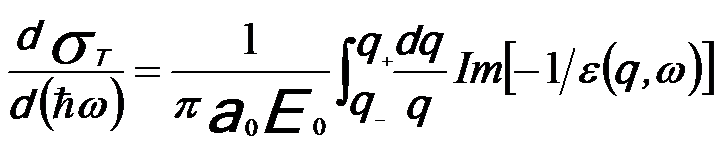 ------ [4436e]
------ [4436e] 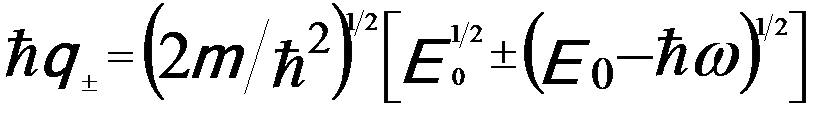 ------ [4436f]
------ [4436f] 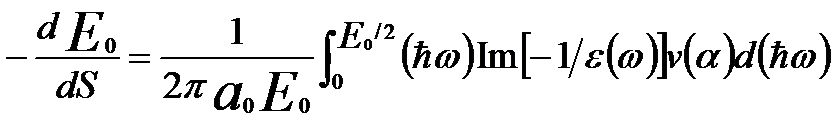 ------ [4436g]
------ [4436g]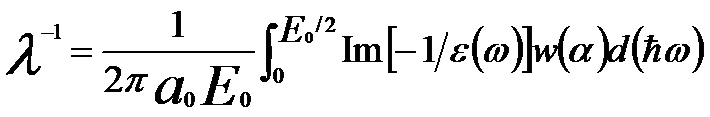 ------ [4436h]
------ [4436h]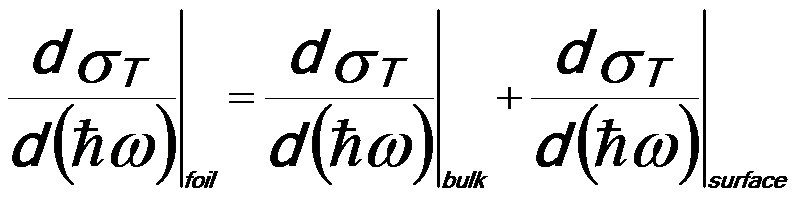 ------------ [4436i]
------------ [4436i]