=================================================================================
In general, the Point Spread Function (PSF) describes the response of an imaging system to a point source or point object. Figure 4907 shows a simple example of the effect of a PSF.

Figure 4907. A simple example of the effect of a PSF.
In Figure 4907, the relationship among W, p and H can be given by,
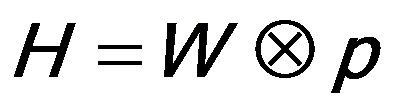 ------------------------------- [4907a] ------------------------------- [4907a]
where,
H -- The obtained image,
W -- The true (non-degraded) image,
p -- The Point Spread Function of the system.
Figure 4907 indicates the obtained image H is blurry due to the "bad" PSF p.
The probe forming aperture in STEM is often compared to the objective aperture in parallel beam illumination in CTEM. The effect of aperture size on the CTF for HAADF STEM imaging is a much more complex issue. The PSF is a measurement of the energy spread of the system and is proportional to the square of the probe wavefunction but not the wavefunction itself (as in bright field CTEM). The response to increasing the aperture size is non-linear and affects all spatial frequencies, not just the highest. The phase errors at large angles to the optic axis essentially are mixed in to the lower frequencies, degrading both contrast and image localization.
The response characteristics of an imaging system to a point source or object can be described by PSF. In imaging mode of electron or optical microscopes, the point spread in an imaging plane is determined by information limit and thus, the image intensity can be given by,
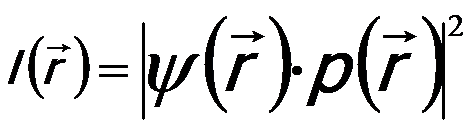 --------------------------------------- [4907b] --------------------------------------- [4907b]
where,
ψ(r) -- The exit wave function,
p(r) -- The point spread
function of the objective aperture or the virtual
aperture.
For EELS analysis, the final energy resolution of the system is limited by the energy spreads of the beam at the electron source and due to the spectrometer optics. The resulting “degraded” spectrum can still be given by Equation 4907a but with different assigned meaning:
(i) H -- The acquired spectrum,
(ii) W -- The true (non-degraded) spectrum,
(iii) p -- The Point Spread Function of the system including the electron source and EELS units.
Ignoring any specimen interaction, as the electron beam passes through the spectrometer, the energy distribution of the beam still gains a long-tail from the optical aberrations. This additional spread is classical PSF of the system. In order to record a correct PSF, the contributions from different components of the electron optic system to the final energy spread must be understood, for instance, by modeling the distribution of electrons emitted by the source and subsequent spreading introduced by the EEL spectrometer optics in terms of EELS analysis. However, the point spread function of the probe can also be calculated by Fourier transforming and squaring the wavefunction in terms of imaging.
The natural line width of the emitted X-rays (e.g. Mn Kα line) in EMs (electron microscopes) is only a few eV but the line widths obtained with EDS systems are normally larger than 100 eV, for instance, the EDS-detected FWHM (full width at half maximum) at the energy of Mn Kα is 135-165 eV. The natural energy distribution of the characteristic X-rays of a single line is well described by the Lorentzian probability distribution instead of Gaussian shape obtained by the energy-dispersive detectors. The electronic noise in the EDS system introduces the peak broadening that is a major source causing the difference between the EDS-detected and natural energy resolutions. The width of the electronic noise is also described as the ‘point-spread function’ of the detector.
|
