=================================================================================
Unlike other more direct forms of imaging, holography
(using electromagnetic, electron, or other kinds of
radiation) is a two-step process (shown in Figure 2560a):
i) Record interference fringes with an objective wave and a reference wave (hologram) as mentioned above. This pattern can be stored in a digital or analogue medium.
ii) Reconstruct the hologram using a light beam or a Fourier transformation [1]. To obtain an image of the object, in this second step we need to process the hologram by illuminating it with a wave identical to the reference wave used in step i). The second step is
customarily called reconstruction. Practically, this step is performed with a personal computer (PC) by restoring the electron wave as a numerical wave that is analyzed by sophisticated wave optical methods.
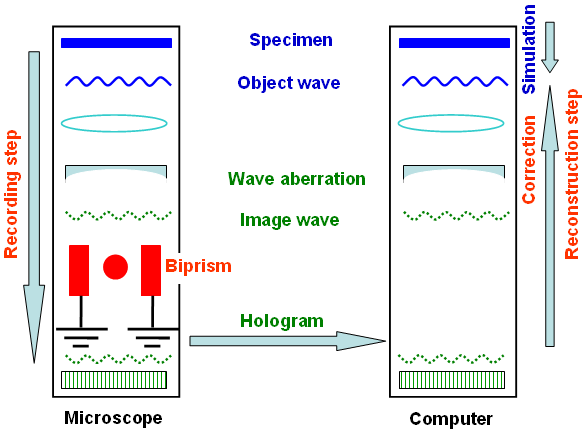
Figure 2560a. Schematic illustration of the two-step holography procedure.
In the second step of electron holography analysis, the electron hologram (Figure 2560b (a)) recorded in TEM is reconstructed with the proper laws of wave optics on a personal computer (PC) [2,3]. The reconstruction process starts with the Fourier transformation of the hologram, producing a centerband and two sidebands that represent the Fourier transform of the complete image wave and its complex conjugate, respectively. [4] Both sidebands are identical except for the sign of the image phase. In this way, the amplitude and phase information of the electron exit wave are extracted from the recorded electron holograms by using digital Fourier transform as well as side band filtering [4]. The Fourier transformation of the hologram Ihol gives the complex spectrum (Figure 2560b (b)) by, [4]
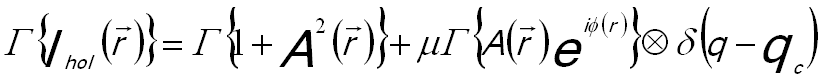
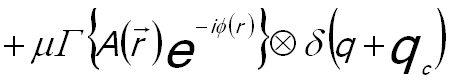 ------------------------ [2560a] ------------------------ [2560a]
where,
|qc| -- (=kβ'), the carrier frequency of the interference
fringes,
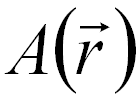 -- The amplitude, -- The amplitude,
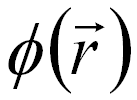 -- The phase, -- The phase,
µ -- The fringe contrast.
The first term on the right of Equation 2560a is called "centerband", representing the diffractogram of a conventional
electron micrograph. The second and third terms correspond
to the complex diffraction pattern and their complex
conjugate and are "sideband + 1" and "sideband - 1", respectively. The sideband + 1 is cut out and centered to the origin in Fourier space as shown in Figure 2560b (d).
The inverse Fourier transformation produces the reconstructed image wave, containing both amplitude (A(r)) (shown in Figure 2560b (e)) and phase (ϕ(r)) (shown in Figure 2560b (f)) information,
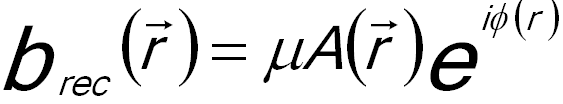 ------------------------ [2560b] ------------------------ [2560b]

Figure 2560b. Image wave reconstruction demonstrated at a hologram
of Si3N4 in [001]-orientation. Adapted from [4]
Unlike the negligible distortions in most CTEM analyses, distortions extremely affect off-axis electron holograms as the phase information is encoded in the bending of the interference fringes [3-5]. The origin of the distortions in off-axis electron holograms are projector lenses, local variations in TEM specimen thickness, charging of the biprism filament, and shear distortion of the fiber optic of the CCD camera. [4] The distortion-induced phase modulation can normally be automatically corrected within the reconstruction process by using a reference hologram, taken by removing the specimen from the field of view using the goniometer of the microscope and without changing the optical parameters. In other words, this process compensates the geometric distortions caused by the imaging and recording system. The reference phase is subtracted from the image phase in order to correct the distortion-induced phase modulations. Furthermore, the aberrations of the reconstructured image wave can more accurately be corrected by multiplying the complex diffraction pattern of the reconstructed image wave brec(r) by the factor of the wave aberration function.
[1] Y Y Wang, M. Kawasaki, J. Bruley, M. Gribelyuk, A. Domenicucci, and
J. Gaudiello, Off-axis electron holography with a dual-lens
imaging system and its usefulness in 2-D potential mapping of semiconductor
devices. Ultramicroscopy 101: 63–72 (2004).
[2] Franke, F.J., Herrmann, K.-H. & Lichte, H. (1988). Numerical
reconstruction of the electron object wave from an electron
hologram including the correction of aberrations, Scan Microsc
Suppl 2, 59–67.
[3] Rau, W.-D., Lichte, H., Völkl, E. & Weierstall, U. (1991).
Real-time reconstruction of electron-off-axis holograms recorded
with a high pixel CCD camera. J Comput-Assist Microsc
3, 51–63.
[4] Michael Lehmann, and Hannes Lichte, Tutorial on Off-Axis Electron Holography, Microsc. Microanal. 8, 447–466, 2002.
[5] Völkl, E. & Lehmann, M. (1999). The reconstruction of off-axis
electron holograms. In Introduction to Electron Holography,
Völkl, E., Allard, L.F. & Joy, D.C. (Eds.), pp. 125–151. New York:
Kluwer Academics/Plenum Publishers.
|

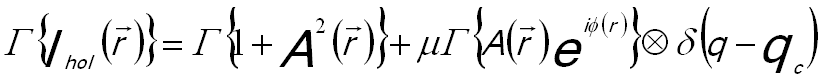
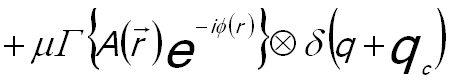 ------------------------ [2560a]
------------------------ [2560a] 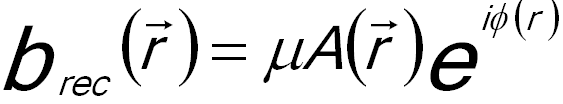 ------------------------ [2560b]
------------------------ [2560b] 